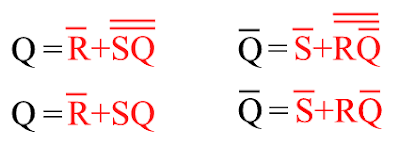Cuando la entrada A y la salida son inicialmente "cero" ("0"), el bloque OR está alimentado con dos ceros, produciendo la salida de cero.
Cuando activamos la entrada con un valor de A=1, el bloque OR producirá una salida de "1", lo cual pondrá una entrada de "1" en el mismo bloque OR compatible con la salida de "1".
Al volver a tomar la entrada A su valor de cero, el "1" a la entrada del OR producido por su salida mantendrá la salida del OR en el estado "1". Esto es, cuando A toma el valor de "1", la salida toma también el valor de "1" y permanece en ese estado por tiempo indefinido aún cuando A regrese a su valor original de "0".
Este ejemplo demuestra una característica interesante e importante que juega la retroalimentación (feedback) en los circuitos lógicos. La retroalimentación proporciona memoria a los circuitos lógicos.
Un diagrama de tiempos característico del comportamiento del circuito sería como el siguiente:
Una forma de "limpiar el registro" (esto es, borrar la memoria) es añadiendo unos componentes de la siguiente manera:
Cuando no hay ninguna señal en R (o sea, cuando la entrada en la terminal R es R=0), por la acción del NOT inversor el bloque AND conectará directamente la salida del bloque OR a la entrada del mismo y no tendrá efecto alguno en el diagrama de tiempos del circuito previo. Este circuito se comportará exactamente como el circuito anterior.
Sin embargo, cuando se aplica una entrada de "1" a R, la compuerta AND interrumpirá la alimentación de la salida del OR a la entrada del mismo, "borrando" la memoria si es que la salida era "1" y la terminal S tenía el valor de "0". En el caso de que R permanezca activada con un "1", la salida tomará directamente el valor de S.
Obsérvese que arriba se llevó a cabo un ligero cambio en la notación de las terminales de entrada del circuito. A la entrada que lo puede "ajustar" con una salida de "1" se le ha designado con la letra S, una abreviatura de la palabra inglesa Set que significa precisamente "ajuste", mientras que a la terminal con la cual se puede "reajustar" el circuito "limpiando" el registro previo se le ha designado con la letra R, una abreviatura de la palabra inglesa Reset que significa precisamente "reajuste". Esto se ha hecho para ir adecuando nuestra notación con la notación utilizada en la mayoría de la literatura técnica.
Un diagrama de tiempos ilustrando todas las situaciones posibles se muestra a continuación:
La función de "limpieza de registro" es indispensable en una configuración de circuitos lógicos para borrar información previa y poder procesar información nueva.
PROBLEMA: El Flip-Flop R-S. Analizar el siguiente circuito considerando todas las 16 combinaciones posibles de unos y ceros (cuatro a la entrada y cuatro a la salida) descartando aquellos estados que resulten incompatibles. Asimismo, construír una Tabla de Verdad lo más simplificada posible para dicho circuito.
El análisis se llevará a cabo haciendo un diagrama independiente para cada una de las combinaciones posibles, trazando el flujo de los valores binarios y observando la compatibilidad de los mismos para cada combinación de valores. Empezaremos con la primera combinación en la cual supondremos que tanto las dos entradas R y S como las dos salidas Q y Q tienen valores de cero:
R=0, S=0, Q=0, Q'=0
El 0 que suponemos a la salida del NAND superior alimenta con dicho 0 una de las entradas del NAND inferior, el cual junto con el 0 que está siendo puesto en la terminal S producirá un 1 a la salida Q' del NAND inferior. Este 1 es incompatible con el valor de 0 que estamos asumiendo para Q'. Por otro lado, el 0 que suponemos a la salida del NAND inferior alimenta con dicho 0 una de las entradas del NAND superior, el cual junto con el 0 que está siendo puesto en la terminal R producirá un 1 a la salida Q del NAND superior. Este 1 es incompatible con el valor de 0 que estamos asumiendo para Q. Por lo tanto, se descarta por completo esta combinación de valores por no ser una combinación válida.
R=0, S=0, Q=0, Q'=1
En este caso, de nueva cuenta el 0 que suponemos a la salida del NAND superior alimenta con dicho 0 una de las entradas del NAND inferior, el cual junto con el 0 que está siendo puesto en la terminal S producirá un 1 a la salida Q' del NAND inferior. Este 1 sí es incompatible con el valor de 1 que estamos asumiendo para Q'. Sin embargo, por otro lado, el 1 que suponemos a la salida del NAND inferior que alimenta con dicho 1 una de las entradas del NAND superior, junto con el 0 que está siendo puesto en la terminal R producirá un 1 a la salida Q del NAND superior. Este 1 es incompatible con el valor de 0 que estamos asumiendo para Q. Por lo tanto, también se descarta esta combinación de valores por no ser una combinación válida.
R=0, S=0, Q=1, Q'=0
Podemos ver que este caso es similar al caso anterior, lo cual era anticipable por la simetría de la figura.
R=0, S=0, Q=1, Q'=1
Al seguir el flujo de todas las señales con los valores supuestos, encontramos que en este caso los valores sí son compatibles. Por lo tanto, podemos hacer la siguiente Tabla de Verdad para los mismos:
R=1, S=0, Q=0, Q'=0
Nuevamente, encontramos otra situación en la que la combinación de valores no es compatible, razón por la cual se descarta esta posibilidad.
R=1, S=0, Q=1, Q'=0
Esta combinación de valores también se descarta por no ser una combinación compatible.
R=1, S=0, Q=0, Q'=1
Los valores en este caso sí son compatibles, y por lo tanto podemos hacer una Tabla de Verdad para los mismos:
R=1, S=0, Q=1, Q'=1
Esta es una combinación de valores que no es compatible, y por lo tanto se descarta.
R=1, S=0
Antes de proseguir, para ahorrarnos trabajo podemos explotar a nuestro favor una simetría. Puesto que el circuito es simétrico en el sentido de que si tomamos lo volteamos por completo de arriba abajo tendremos en esencia lo mismo, al tratar los cuatro casos correspondientes a los valores de entrada R=0 y S=1 también estamos cubriendo los cuatro casos correspondientes a los valores de entrada R=1 y S=0 con la simple inversión de los elementos de arriba hacia abajo. En base a la simetría y los resultados obtenidos previamente, podemos afirmar que el único conjunto de valores compatibles para R=0 y S=1 es Q=1 y Q'=0, lo cual podemos resumir en la siguiente Tabla de Verdad:
Podemos proseguir con las combinaciones de valores faltantes:
R=1, S=1, Q=0, Q'=0
Esta combinación de valores se descarta por ser totalmente incompatible.
R=1, S=1, Q=0, Q'=1
En este caso la combinación de valores sí es compatible, y su Tabla de Verdad es:
R=1, S=1, Q=1, Q'=0
Los valores en este caso también son compatibles, y su correspondiente Tabla de Verdad será:
Falta ya tan sólo una combinación posible de valores por checar. Es la siguiente:
R=1, S=1, Q=1, Q'=1
Así, la última combinación posible de valores que nos faltaba por checar resulta ser totalmente incompatible, razón por la cual también se descarta.
Podemos juntar ahora todas las Tablas de Verdad para este circuito en una sola:
aPara simplificar esta Tabla de Verdad, como primera observación se nota que el único caso en el cual los valores de Q y Q' no son complementarios es R=0 y S=0. En la terminología técnica empleada en el estudio de los circuitos lógicos, este es un estado es conocido como un estado no-definido. Con esto en mente, y agrupando las salidas similares por razones que pronto quedarán claras, la Tabla de Verdad toma el siguiente aspecto:
Analizando esta Tabla de Verdad, encontramos algunos detalles interesantes. Si las entradas toman los valores R=1 y S=0, las salidas tomarán los valores Q=0 y Q'=1. Y si las entradas cambian a los valores R=0 y S=1, las salidas cambiarán a los valores Q=1 y Q'=0. Esto es, cuando las entradas son complementarias, Q toma el valor de S.
Al tomar las entradas los valores R=1 y S=1; existen dos salidas complementarias válidas. Esto indica que al tomar ambas R y S el valor de 1, se retendrán a la salida los valores de la condición previa, esto es, el circuito "recordará" su estado anterior. Por ejemplo, si la entrada tiene los valores R=1 y S=0, la salida tomará los valores Q=0 y Q'=1. Al tomar la entrada los valores R=1 y S=1, la salida seguirá reteniendo los mismos valores Q=0 y Q'=1. La única manera de invertir la salida Q es aplicando la condición R=0 y S=1. Después de aplicar dicha condición, el circuito mantendrá la salida de Q=1 y Q'=0 al aplicársele la condición R=1 y S=1.
Puesto que en el estado R=1 y S=1 las salidas pueden tomar dos valores que siempre serán complementarios, podemos simplificar aún más la Tabla de Verdad:
Esta Tabla nos quiere decir que para la condición R=1 y S=1, si Q toma el valor de 1 entonces Q' tomará el valor de 0 o bien, si Q toma el valor de 0 entonces Q' tomará el valor 1.
Nótese que cuando R y S son complementarios, el valor de S es igual al valor de Q y el valor de R es igual al valor de Q'. Tomando esto en consideración, se acostumbra invertir de la siguiente manera las terminales de entrada para que estén de acuerdo con el orden en la figura de los valores que toman las terminales de salida:
Frecuentemente, este circuito se encierra en una "caja negra" representándosele de la siguiente forma:
Este bloque se conoce comúnmente como el Flip-Flop R-S, aunque también se le conoce ampliamente como un R-S latch, y desempeña un papel importante en los circuitos lógicos.
El comportamiento de un flip-flop R-S (y de hecho el comportamiento de cualquier circuito lógico secuencial capaz de pasar de un estado estable a otro) puede ser descrito con un diagrama de tiempos como el siguiente, en el cual el paso del tiempo ocurre de izquierda a derecha:
En este diagrama de tiempos, al principio de la "acción" ambas terminales de entrada S y R están puestas a un valor de "1" lógico, mientras que se supone que la salida Q se encuentra en un estado estable de "0". Como podemos ver, la terminal R recibe un descenso de "1" a "0" seguida de un ascenso que la regresa a su valor de "1", pero esto no produce efecto alguno en la salida puesto que para ello es la terminal S la que tiene que ser activada. Esto es precisamente lo que se lleva a cabo a continuación, y podemos ver que al caer S de "1" a "0" la salida Q cambia de inmediato de "0" a "1". Tras esto, la terminal S es llevada de "0" a "1", y nuevamente se le aplica otro descenso, pero en esta ocasión ya no tiene efecto alguno sobre la salida Q, su efecto ya se dejó sentir anteriormente. Por último, con la salida Q ajustada a "1", la terminal R es llevada de "1" a "0", y en esta ocasión si produce un efecto inmediato, "reajustándose" la salida de Q a un valor de "0". Este diagrama de tiempos resume prácticamente todas las condiciones posibles que describen el comportamiento del circuito, como debe hacerlo un buen diagrama de tiempos.
Podemos construír un flip-flop con bloques NAND, o podemos procurarlo ya construído en un componente como el circuito integrado 4044, el cual incluye cuatro flip-flops NAND por el precio de uno solo:
PROBLEMA: Usando álgebra Boleana, encontrar expresiones para las salidas en función de las entradas, simplificando las expresiónes resultantes lo más que se pueda, para un Flip-Flop construído con bloques NAND. Asimismo, constrúyase una Tabla de Verdad para el circuito usando las expresiones obtenidas.
Trazando el flujo de señales para un flip-flop construído con bloques NAND, se ve que las salidas deberán ser como se muestra en el siguiente diagrama:
Las expresiones Boleanas para las salidas son:
Introduciendo cada expresión en la otra para tener las salidas en función de las entradas R y S exclusivamente:
Usando la ley de DeMorgan A · B = A + B para simplificar ambas expresiones:
Con las expresiones anteriores podemos introducir valores de R y S para construír una Tabla de Verdad:
R=0, S=0:
Q = 0 + 0 • QR=0, S=1:
Q= 1
Q = 0 + 0 • Q
Q = 1
Q = 0 + 1 • QR=1, S=0:
Q = 1 + Q
Q = 1
Q = 1 + 0 • Q
Q = 0 + 0
Q = 0
Q = 1 + 0 • QR=1, S=1:
Q = 0 + 0
Q = 0
Q = 0 + 1 • Q
Q = 1 + Q
Q = 1
Q = 1 + 1 • QLlamando al estado en el cual los valores de Q y Q no son complementarios (R=0 y S=0) un estado no-definido, podemos construír la Tabla de Verdad con la información obtenida:
Q = 0 + Q
Q = Q
Q = 1 + 1 • Q
Q = 0 + Q
Q = Q
Esta es la misma Tabla de Verdad que la obtenida en el problema anterior, excepto que aquí se obtuvo por una vía mucho más rápida, sin tener que probar todas las combinaciones posibles de "unos" y "ceros" en las entradas R y S y en las salidas Q y Q. Nuevamente, la enorme efectividad del álgebra Boleana como herramienta de simplificación muestra su potencia matemática.
PROBLEMA: Usando álgebra Boleana, encontrar expresiones para las salidas en función de las entradas, simplificando lo más que se pueda, para el siguiente flip-flop R-S construído con bloques NOR:
Asimismo, constrúyase una Tabla de Verdad para el circuito usando las expresiones obtenidas.
Trazando el flujo de señales para un flip-flop R-S construído a base de bloques NAND, se ve que las salidas deberán ser como se muestra a continuación:
Las expresiones Boleanas para las salidas son:
Introduciendo cada expresión en la otra para tener las salidas en función de las entradas R y S exclusivamente:
Usando la ley de DeMorgan A + B = A · B para simplificar ambas expresiones:
Con las expresiones anteriores podemos introducir valores de R y S para construír una Tabla de Verdad:
R=0, S=0:
Q = 0 (0 + Q)R=0, S=1:
Q= 1 • Q
Q= Q
Q = 0 (0 + Q)
Q= 1 • Q
Q = Q
Q = 0 (1 + Q)R=1, S=0:
Q = 1 (1)
Q = 1
Q = 1 (0 + Q)
Q = 0 (Q)
Q = 0
Q = 1 ( 0 + Q)R=1, S=1:
Q = 0 (Q)
Q = 0
Q = 0 (1 + Q)
Q = 1 (1)
Q = 1
Q = 1 (1 + Q)Llamando al estado en el cual los valores de Q y Q no son complementarios (R=1 y S=1) un estado no-definido, podemos construír la Tabla de Verdad con la información obtenida:
Q = 0 (0)
Q = 0
Q = 1 (1 + Q)
Q = 0 (1)
Q = 0
Comparando esta Tabla de Verdad con la obtenida en el problema anterior para un flip-flop R-S construído con bloques NAND, encontramos que son casi idénticas excepto por una diferencia: mientras que para un flip-flop R-S construído con bloques NAND la condición en la cual el flip-flop entra en un estado indefinido está dada por R=0 y S=0, para el flip-flop R-S construído con bloques NOR la condición en la cual el flip-flop entra en un estado indefinido está dada por R=1 y S=1. Asimismo, la condición en la cual el flip-flop R-S construído con bloques NAND "recuerda" su estado anterior es R=1 y S=1, mientras que para el flip-flop construído con bloques NOR la condición en la cual el flip-flop "recuerda" su estado anterior es R=0 y S=0.
Podemos construír un flip-flop con bloques NOR, o podemos procurarlo ya construído en un componente como el circuito integrado 4043, el cual incluye cuatro flip-flops NOR por el precio de uno solo:
A menos de que se indique lo contrario, en todos los problemas restantes de aquí en adelante se utilizarán exclusivamente flip-flops R-S hechos con bloques NOR.