PROBLEMA: Encontrar las modificaciones externas requeridas por un flip-flop R-S hecho con bloques NAND para que se comporte como si fuera un flip-flop hecho con bloques NOR.
Requerimos un bloque que transforme las entradas del flip-flop hecho con bloques NAND en la manera como se muestra a continuación:
Tomando en cuenta las características del flip-flop R-S hecho con bloques NOR y los requerimientos del flip-flop hecho con bloques NAND, las entradas y salidas del bloque transformador (mostrado de color ciano) deben estar relacionadas según se muestra en la siguiente Tabla de Verdad de dos entradas y dos salidas, obtenida mediante la técnica de los minterms:
de la cual obtenemos las siguientes relaciones:
S = SERE + SERE
S = (SE + SE)RE
S = RE
R = SERE + SERE
R = SE(RE + RE)
R = SE
La configuración requerida toma entonces el siguiente aspecto:
Si encerramos todo esto dentro de una "caja negra" y se lo damos a un técnico para que haga las pruebas necesarias para determinar qué clase de flip-flop es, el técnico creerá que se trata de un flip-flop R-S hecho con bloques NAND. A menos de que sea un técnico realmente bueno y no se deje llevar tan sólo por las apariencias.
PROBLEMA: Analizar el siguiente circuito.
Para llevar a cabo el análisis, supóngase que inicialmente Bin=0, A=0 y Bout=0.
Con A=0 y Bin=0, las salidas del AND 1 y del AND 2 deben ser ambas "1", entradas con las cuales el flip-flop R-S mantiene su estado de Bout=0. que aquí suponemos válido. Al tomar Bin el valor "1", las salidas de los dos AND siguen siendo "1" y el flip-flop seguirá reteniendo su estado Bout=0. Esto es, no importa el valor que tome Bin, éste no podrá afectar al flip-flop mientras la terminal A permanezca en la condición A=0. Si el flip-flop tuviera una salida Bout=1, esta también permanecerá constante ante cambios de Bin siempre y cuando la terminal A permanezca en "0".
Suponiendo que ahora la terminal A toma el valor de "1" observamos que las entradas al flip-flop serán complementarias y sus valores dependerán del valor que tome Bin. En este estado, si aplicamos un "1" a Bin, el AND 1 producirá una salida de "0" y el AND 2 producirá una salida de "1", lo cual pondrá al flip-flop en el estado Bout=1. Removiendo el "1" de la terminal A primero y el "1" de la terminal Bin después, las salidas de los AND 1 y 2 serán "1", con lo cual el flip-flop retendrá el valor Bout=1. Sin el "1" en la terminal A, no importa que valor tome Bin, la salida seguirá siendo Bout=1. Esto es, al activar la terminal de acceso A, el circuito conservará en su memoria (a la salida Bout) el valor que le hayamos aplicado a Bin durante el período de tiempo que duró activada la terminal A. Si el bit de entrada Bin es "0", basta activar por un corto tiempo la terminal A para "grabar" dicho bit en el circuito, pudiendo leer el bit a la salida Bout cuantas veces se desee tiempo después de que se haya desactivado la terminal A. Si deseamos "grabar" el bit "1", entonces lo ponemos en la terminal de entrada Bin y activamos la terminal de acceso A por un tiempo corto, después del cual el bit está disponible a la salida Bout para ser leído cuantas veces se desee. Este es básicamente un circuito para almacenar un bit de información por tiempo indefinido.
Un diagrama de tiempos ilustrando todas las combinaciones secuenciales posibles es el siguiente:
PROBLEMA: El RAM (la Memoria de Acceso al Azar). Supóngase que existe un arreglo rectangular de flip-flops ordenados en un acomodo rectangular de 3 por 5 cuadros, cada cuadro conteniendo un flip-flop. Ilustrar la manera en la cual se pueda localizar un flip-flop cualquiera en un momento dado. Ilustrar también la manera en la cual se puede introducir y saca información de dicho flip-flop.
El arreglo más probable sería el siguiente:
Supóngase que deseamos encontrar el elemento mostrado en la figura. Para ello bastará con activar las terminales que lo localizan, que en este caso equivale a poner X3=1 y Y4=1, dejando un "0" en todas las demás terminales.
Siguiendo la convención del problema anterior, Bout es el bit ya almacenado por un flip-flop seleccionado, mientras que Bin es el bit a ser almacenado por el flip-flop seleccionado.
Podemos ver en el diagrama que la terminal Bin va dirigida hacia cada elemento del arreglo rectangular, cada uno de los cuales será llamado célula básica o celda para nuestros propósitos, mientras que la terminal Bout viene conectada desde cada célula. Asimismo, la terminal "Escribir/Leer" está también conectada a cada célula.
El diagrama de una célula básica es el siguiente:
Dentro de cada célula estamos utilizando la configuración estudiada en el problema anterior (la cual tomamos como "caja negra" y no se muestra en detalle para simplificar este diagrama esquemático).
Empezamos suponiendo que para la célula arriba mostrada, X3=1 y Y4=1, esto es, estamos domiciliando dicha célula, la célula especificada por las "coordenadas" X3 y Y4. Esto implica que la salida del AND1 es "1". Si otra célula fuese la localizada, entonces tendríamos Xn ó Yn ó ambos, con lo cual la salida del AND sería entonces "0".
Para analizar el comportamiento de la célula básica, estudiamos dos casos diferentes:
a) La terminal R/W (Read/Write, que en español se traduce como "Escribir/Leer") está desactivada con un "0". En este caso, la salida del AND 2 es "0", lo cual implica que la terminal de acceso A está desactivada y la información contenida por el flip-flop (Bo) permanece inalterada. Al mismo tiempo, el AND 3 está activado y su salida Bo dependerá de la información Bo previamente almacenada en el flip-flop. Estamos, por lo tanto, leyendo información de la célula localizada. Esta es la función R (Read) de lectura.
b) La terminal R/W es activada con un "1". En este caso, la salida del AND 2 es "1", lo cual implica que la terminal de acceso A está activada. La salida Bo del flip-flop (que es la salida Bo de la célula) dependerá del valor que tome Bi. Podemos, por lo tanto, escribir información en la célula localizada; esta es la función W (Write) de escritura, después de lo cual desactivamos la terminal R/W poniéndole nuevamente un "0" para poder preservar dicha información.
PROBLEMA: Una memoria RAM tiene una capacidad de 8 por 8 bits. ¿Cómo se puede seleccionar cada bit sin usar un gran número de terminales fuera del RAM?
Antes de continuar, identificaremos cada terminal de entrada de selección del RAM con un número binario diferente (al cual se le llamará "domicilio" o adresss) como se muestra a continuación:
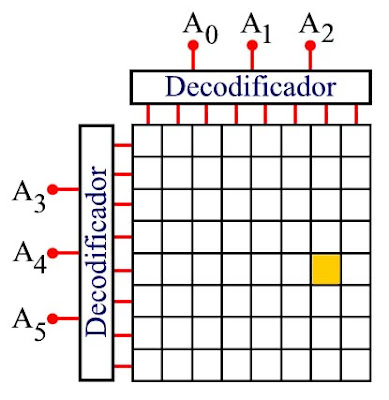
No se ha mostrado en el diagrama la terminal bi-direccional de "Escribir/Leer" (Read/Write) con la cual se escribe un bit dentro de los flip-flops seleccionados. Obsérvese que en cada caso (domicilios horizontales, domicilios verticales) se escogió una numeración binaria ascendente tanto para los domicilios horizontales como para los verticales. Podemos añadir ahora un decodificador binario en cada lado para tener entonces el siguiente circuito:
Podemos observar que con este arreglo, el número de terminales requeridas para encontrar un determinado bit (o mejor dicho, un determinado flip-flop que está almacenando un bit que puede ser un "0" o un "1") se reduce grandemente. En las figuras se ha mostrado el flip-flop identificado por las combinaciones A0A1A2=110 y A3A4A5=100 (o bien, por la palabra A0A1A2A3A4A5=110100, que es lo que comunmente se acostumbra usar.
El esquema de domiciliar cada una de las células básicas de una memoria RAM utilizando un arreglo rectangular y reduciendo el número de líneas empleadas para el domiciliamiento con la ayuda de un decodificador horizontal y un decodificador vertical es un concepto completamente general, independiente de la tecnología empleada, ya sea mediante núcleos de ferritas magnéticas o mediante semiconductores o mediante algún otro esquema que aún no ha sido descubierto (ampliar imagen):
En esta representación estamos introduciendo un nuevo concepto con el objetivo de simplificar los diagramas esquemáticos en los cuales varias líneas de conducción eléctrica que llevan información simultánea perteneciente a un mismo grupo de datos son representadas en conjunto como una sola flecha "gorda" en vez de las cuatro u ocho líneas que de otro modo tendrían que ser dibujadas independientemente sin que este exceso de líneas resulte en una mayor claridad de información. Esta "flecha gorda" que aparea datos pertenecientes a información del mismo género es conocida como bus, (posiblemente en similitud con la palabra inglesa con la cual se designa a los camiones públicos utilizados para transportar a varias personas a la vez). Así, el bus que tenemos a la derecha en la siguiente figura representa a las ocho líneas que tenemos a la izquierda de la misma:
PROBLEMA: Ilustrar la forma de conectar varias RAM con una capacidad de 4 por 4 bits cada una para almacenar palabras de 3 bits. ¿Cuál es la capacidad total de memoria del sistema expresada en bits? ¿Cuántas palabras se pueden almacenar?
Puesto que se quiere almacenar palabras de 3 bits de extensión, se requieren tres RAM. Debido a que el arreglo de cada RAM es simétrico (o sea, de 4 por 4 bits) y a que la capacidad horizontal (y la vertical) es una potencia de 2n siendo n=2, podemos usar decodificadores para así tener la siguiente configuración:
Cada RAM tieen una capacidad de 4x4=16 bits. Puesto que se están usando tres memorias RAM de 4 por 4 bits de capacidad cada una, la capacidad total de almacenamiento será de 16 bits por 3, o sea de 48 bits (una capacidad modesta cuando en los inicios del 2007 las capacidades de las memorias RAM a la venta para las computadoras personales de escritorios alcanzaban una capacidad de dos gigabytes, dos mil millones de bits). Obsérvese que si cada RAM tiene integrados sus propios decodificadores (esta es la práctica usual) sin necesidad de que un ingeniero o técnico los tenga que añadir a algún diseño, el arreglo del circuito se simplifica enormemente como se muestra a continuación:
La simpleza de esta configuración sobre la anterior es obvia. La ventaja de usar bloques RAM con decodificadores incluídos en las RAM se hace más obvia aún cuando la cantidad de bloques RAM usados y la capacidad de los mismos va en aumento.
PROBLEMA: Un fabricante anuncia un nuevo tipo de memoria RAM ultra-rápida de 1024 bits hecho a base de tecnología óptica. ¿Cuál es la configuración funcional más probable para tal circuito?
Lo más probable es que sea una RAM de tipo simétrico con las células básicas de información acomodadas en un arreglo rectangular, formada por n bits de cada lado. Podemos, basados en esta información, obtener el número de bits laterales:
n ∙ n = 1024
n² = 1024
n = 32
n² = 1024
n = 32
La RAM parece ser una RAM de 32 bits por 32 bits. Lo más probable también es que use decodificadores en ambos lados con el propósito de reducir las líneas externas de alambrado necesarias para poder llegar a cada célula de información. La extensión de la palabra requerida en cada lado la podemos encontra de la siguiente manera:
2n = 32
log [ 2n ] = log(32)
n ∙ log(2) = log(32)
n = (log 32)/(log 2)
n = (1.50515)/(.30103)
n = 5
n ∙ log(2) = log(32)
n = (log 32)/(log 2)
n = (1.50515)/(.30103)
n = 5
El resultado nos dice que una palabra de tan sólo cinco bits contendrá 32 combinaciones posibles de "unos" y "ceros".
La RAM tendrá entonces la siguiente configuración:
El "bit" a ser leído con la operación de lectura R (poniendo un "0" en la terminal R/W) será leído de la terminal Bo, mientras que el "bit" a ser escrito con la operación de escritura W (poniendo un "1" en la terminal R/W) será puesto en la terminal Bi.
PROBLEMA: La ROM (Memoria de Lectura Unicamente). Analizar el siguiente circuito construyendo una Tabla de Verdad para el mismo.
El primer paso para analizar este tipo de circuito es introducir todas las combinaciones posibles de "unos" y "ceros" en las terminales de entrada A, B y C. Por ejemplo, con la combinación AB=00, únicamente se activa la línea L1. De la misma manera, con cada una de las combinaciones restantes se activa únicamente una de las líneas L2, L3 y L4. No nos debe llevar mucho tiempo el reconocer que lo que tenemos dentro del recuadro de línea roja es nada menos que un decodificador. Las salidas H1, H2, H3 y H4 se pueden obtener de inmediato de los ORs sabiendo que únicamente una de las líneas L puede estar activada en un momento dado. Tomando esto en consideración, la Tabla de Verdad obtenida será como la que se muestra a continuación:
Podemos ver que cada combinación de "unos" y "ceros" a la entrada siempre producirá la misma combinación de "unos" y "ceros" que le corresponda a la salida a dicha entrada, determinado por las conexiones internas en el circuito. Esto, en cierta forma, es equivalente a una "memoria", la cual está contenida dentro del recuadro de línea verde. Sin embargo, este tipo de memoria es diferente a las demás en el sentido de que únicamente se pueden leer palabras binarias de la misma. No se pueden grabar palabras nuevas en este tipo de memoria sin cambiar el alambrado interno del circuito. Es por esto que esta memoria es conocida comúnmente como Memoria de Lectura Unicamente (Read Only Memory ó ROM), ya que únicamente se pueden leer palabras de este memoria, no se pueden grabar palabras en la misma.
El ROM ofrece una configuración almacenada de "unos" y "ceros" que puede ser utilizada de la misma manera que un programa almacenado en la memoria de una computadora digital. La secuencia de eventos lógicos puestos en movimiento por esta configuración almacenada de datos recibe el nombre de microprograma. Asismismo, cada evento lógico especificado en los domicilios de un microprograma recibe el nombre de microinstrucción.
PROBLEMA: Tomando en cuenta el circuito del problema anterior, diseñar un ROM que posea la siguiente Tabla de Verdad:
La configuración pedida tiene el siguiente aspecto:
PROBLEMA: Describir la forma en la cual trabaja la Memoria ROM cuyo diagrama esquemático es el siguiente:
La forma (simbólica) en la cual trabaja esta memoria ROM de acuerdo con lo que podemos leer en este diagrama esquemático es la siguiente:
Cuando todos los interruptores eléctricos en el extremo izquierdo del diagrama están abiertos tal y como se muestra arriba, no entra ningún voltaje (ningún "1") en ninguna de las terminales de entrada A0, A1, A2 y A3, siendo por lo tanto la entrada "0" en todas ellas. Así, cuando la palabra de entrada es A0A1A2A3=0000, accesamos de la memoria ROM su contenido puesto en una de sus "celdas", que es el dato 4D (dado en notación hexadecimal, equivalente a 01001101 en notación binaria). Este dato es puesto en las líneas de salida del ROM como el byte:
D7D6D5D4D3D2D1D0= 01001101
tal y como lo muestra el diagrama. Si queremos accesar otro contenido dentro del ROM, por ejemplo el contenido que está puesto bajo el domicilio A0A1A2A3=0011 entonces cerramos los interruptores eléctricos que corresponden a las líneas de entrada A0 y A1, con lo cual el voltaje que tomamos como "1" pasa directamente a dichas líneas. Junto con los ceros en las demás entradas, esto pone el domicilio 3 (0011) en la entrada A0A1A2A3, lo cual accesa el contenido en el domicilio 3 que es 6D, el cual será puesto a la salida del ROM.
Este ROM tiene capacidad suficiente para almacenar 16 bytes.
Este circuito fue tomado de la página Internet de Educypedia. La acción animada de este ROM "trabajando" se puede ver yendo al siguiente domicilio:
http://www.ibiblio.org/kuphaldt/socratic/output/animation_ROM_memory_fast.gif
PROBLEMA: El código ASCII. Una de las desventajas del indicador luminoso de 7 segmentos es que no se pueden representar las letras del alfabeto en el mismo. Este problema se soluciona empleando una matriz (arreglo rectangular) de 5 por 7 diodos LED, cada uno en forma de punto. Representar la expresión A+B usando este tipo de indicadores. Bajo el código ASCII, se pueden representar hasta 64 caracteres diferentes si se usa un ROM para almacenar la combinación particulas de "unos" y "ceros" correspondientes a cada caracter. ¿Cuál es la capacidad total en bits requerida del ROM? ¿Cuál es su configuración más probable?
Usando tres matrices de diodos LED indicadores, la expresión A+B tendrá un aspecto como el siguiente:
Para representar cada caracter se requieren 7 por 5 bits, o sea 35 bits. Puesto que en el código ASCII hay un total de 64 caracteres, o sea 64 combinaciones diferentes de "unos" y "ceros", se concluye que la capacidad total de almacenamiento requerida del ROM es de 35x64 = 2240 bits.
Puesto que 64 es un múltiplo de 2n, en lugar de usar 64 líneas diferentes para obtener cada caracter se puede usar identificación binaria para obtener cada caracter usando un decodificador. Incluyendo el decodificador en el ROM, vemos que el número n de líneas requeridas será:
2n = 64
log(2n) = log(64)
n ∙ log2 = log64
n = (log64)/(log2)
n = (1.80618)/(.30103)
n = 6
log(2n) = log(64)
n ∙ log2 = log64
n = (log64)/(log2)
n = (1.80618)/(.30103)
n = 6
Requerimos de 6 líneas de entrada al decodificador del ROM. Una configuración posible para el ROM requerido sería la siguiente:
La letra A está representada a la salida del ROM como ejemplo del funcionamiento del mismo.