Dada la gran variedad de aplicaciones que encuentra la lógica digital en la práctica, es imposible cubrir todas ellas en una obra limitada como la presente. Posiblemente la aplicación más importante de esta rama de la electrónica sea la computadora digital. Un estudio a fondo sobre este tema queda fuera del alcance de este libro, aunque de cualquier manera se ha incluído información introductoria en los Suplementos puestos al final de esta obra. Se hace hincapié, sin embargo, en el hecho de que podemos construír una computadora digital usando los elementos estudiados en los capítulos anteriores. De cualquier manera, se deja el estudio de dicho tema a obras más especializadas.
Idealmente, en lógica positiva, un "0" lógico equivale exactamente a cero volts, y un "1" lógico equivale exactamente al máximo nivel de voltaje proporcionado por la fuente de poder, y la transición de "0" a "1" ó de "1" a "0" se lleva a cabo de una manera instantánea.
En la práctica, sin embargo, esto no es posible. Conforme las señales digitales van siendo procesadas y van pasando de un circuito a otro, ni el "0" lógico se puede mantener exactamente en cero volts, ni el "1" lógico alcanza a llegar hasta el máximo nivel de volta dado por la fuente de poder que alimenta al sistema. Esto se hace más notorio conforme la velocidad de las señales va aumentando y estas tienen que salir inclusive fuera de la computadora hacia un mundo hostil en donde las interferencias eléctricas y los ruidos generados por motores pesados o aparatos electrodomésticos degradan a la señal agregándole un componente de "ruido" que antes no tenía. Para que las señales digitales del mundo real puedan ser de utilidad, es necesario establecer límites arriba de los cuales un "0" lógico no puede ser considerado ya como tal y debajo de los cuales tampoco un "1" lógico puede ser considerado así. En la siguiente figura en donde podemos distinguir pulso digital, vemos definidas dos bandas amarillas dentro de las cuales el "0" se puede considerar como una señal útil y el "1" también puede ser considerado como una señal útil:
La región intermedia entre estas dos bandas, determinada por el tipo de electrónica que se esté utilizando, es considerada como la "tierra de nadie", y para evitar indefiniciones es necesario incorporar dentro del arsenal de funciones lógicas básicas componentes que sean capaces de "limpiar" una señal ruidosa extrayendo los verdaderos "unos" y los verdaderos "ceros" de todo el ruido circundante, componentes tales como el gatillo Schmitt que será explorado más a fondo en los problemas resueltos.
Frecuentemente, quizá con demasiada frecuencia, al transmitir señales digitales de un punto a otro la señal de cualquier modo pese a los mecanismos compensadores usados para intentar distinguir claramente entre un "0" y un "1" fallan, y en vez de recibirse lo que debería ser un "0" se recibe erróneamente un "1", o en vez de recibirse lo que debería ser un "1" se recibe erróneamente un "0". Es por ello que, además de la electrónica correctora implementada por medio del hardware para tratar de reafirmar un "0" como un "0" y un "1" como un "1", se llevan a cabo procedimientos de detección de errores agregando información adicional a la señal digital.
El mecanismo más frecuentemente utilizado para la detección de errores quizá lo sea la adición del bit de paridad. Esta técnica empezó a tener aplicaciones amplias al utilizarse el código ASCII para transmitir caracteres alfanuméricos de byte en byte. Como el código ASCII no utiliza más de 7 bits para la transmisión de cada caracter ASCII, se puede utilizar como bit adicional el octavo bit de cada byte que normalmente no se utilizaría, una información extra que se considera una redundancia pero que nos permite determinar si ocurrió un error durante el proceso de transmisión. Existen dos variantes del bit de paridad: el bit de paridad par y el bit de paridad impar. El bit de paridad par es puesto como "1" si la cantidad de "unos" en un conjunto dado de bits es impar, haciendo de este modo a la cantidad total de "unos" par. Y el bit de paridad impar es puesto en "1" si la cantidad de "unos" en un subconjunto dado de bits es par, haciendo de este modo al total de "unos" impar. Usando el bit de paridad par, si un caracter ASCII de siete bits que está siendo transmitido tiene un número impar de "unos" como en la palabra 1100001 que contiene tres "unos", entonces se le añade un bit de "1" adicional tranformando a la palabra en 11100001 para que el total de los "unos" en la palabra binaria sea par:
y si la palabra tiene un número par de "unos" entonces se le agrega un "0" para que el total de "unos" de la palabra siga siendo par, como en el caso de la palabra 01100011. De este modo, todos los bytes que están siendo enviados contendrán un número par de bits. Esta adición del "bit de paridad" se hace desde el punto de la transmisión de la señal (que puede ser de una computadora a otra a través de una red o inclusive dentro de la misma electrónica de cada computadora, como cuando se está enviando información del disco duro a la memoria RAM). Al ir llegando cada byte, lo primero que hace el sistema es checar la paridad del byte. Si el número de bits es par, entonces se sabe que la información llegó correctamente, pero si el número de bits es impar, entonces se sabe que ocurrió un error durante el proceso de transmisión del byte, y en tal caso el receptor le pidiría al transmisor envíar de nuevo esa palabra binaria o el paquete completo de palabras binarias dentro del cual está incluído el caracter que llegó erróneo.
La detección de la paridad en el punto receptor se puede llevar a cabo de una manera extremadamente sencilla con un circuito construído a base de un bloque con el cual ya debemos estar familiarizados: el bloque OR-EXCLUSIVO. Por su Tabla de Verdad, sabemos que un OR-EXCLUSIVO de dos entradas A y B dá un "1" cuando ambas entradas son iguales, y dá un "0" cuando ambas entradas son diferentes. Pero ahora veremos al OR-EXCLUSIVO desde otra perspectiva. Cuando ambas dos entradas A y B son iguales, la salida del OR-EXCLUSIVO es "1", o sea cuando las dos entradas son ambas "0" ó cuando las dos entradas son ambas "1", o sea cuando la paridad de la palaba de entrada AB es par. El OR-EXCLUSIVO es capaz de detectar la paridad en una palabra de dos bits, o sea un número par de "unos" cuando hay "unos" en la palabra. ¿Podemos extender este concepto a una palabra binaria de tres bits? La respuesta es afirmativa, y para ello podemos seguir utilizando el mismo OR-EXCLUSIVO de la siguiente manera:
La construcción de la Tabla de Verdad para este circuito, que es la siguiente:
es extremadamente sencilla. Tomamos las entradas combinadas A y B cuando ambas solo están produciendo un "1" a la salida del OR-EXCLUSIVO del cual son entradas (o sea, cuando ambas A y B son iguales). Esta salida de "1" del OR-EXCLUSIVO de arriba es la entrada al OR-EXCLUSIVO de abajo. Y cuando ambas entradas al OR-EXCLUSIVO inferior son iguales, la salida del OR-EXCLUSIVO que es a su vez la salida del circuito será "1", y en caso contrario la salida será "0". Un efecto curioso es que este circuito, el cual tiene una cantidad impar de entradas (tres entradas: A, B y C), produce un "1" a su salida cuando la palabra binaria de entrada ABC es impar (o sea, cuando hay un número impar de "unos" a la entrada), y produce un "0" cuando la palabra binaria de entrada ABC es par. Contrástese esto con el funcionamiento del OR-EXCLUSIVO de dos entradas, cuyo comportamiento es el reverso de esto. Si queremos que se produzca un "1" cuando la paridad de la palabra de entrada sea par (como ocurre con el OR-EXCLUSIVO de dos entradas), todo lo que tenemos que hacer es agregar un inversor lógico NOT a la salida del circuito.
Así como construímos el circuito anterior usando tres bloques OR-EXCLUSIVO, podemos construír otro circuito que incorpore cuatro bloques OR-EXCLUSIVO:
Empleando el mismo razonamiento que el que utilizamos arriba para construír la Tabla de Verdad para el circuito de 3 bits, encontramos que la Tabla de Verdad para el circuito con cuatro bloques OR-EXCLUSIVO es la siguiente:
En este caso, con una cantidad par de entradas, encontramos que el circuito produce un "1" cuando la palabra binaria de entrada ABC es impar, y produce un "0" cuando la palabra binaria de entrada ABC es par.
Este circuito recibe el nombre de árbol de paridad. Podemos extender el mismo concepto con toda facilidad para construír un árbol de paridad de seis bits, o de ocho bits como el árbol de paridad que se muestra a continuación, al cual le hemos dado una salida convencional X y el inverso de la salida, X, con el fin de utilizar la salida "par" como productora de una señal que podemos interpretar y usar en un diseño simplemente como PAR y la salida impar como productora de una señal que podamos interpretar y usar en un diseño simplemente como IMPAR:
Como una cortesía de la Universidad de Hamburgo en Alemania, se encuentra disponible en Internet en el siguiente domicilio un árbol de paridad de ocho bits completamente interactivo, en el que haciendo "clic" con el mouse podemos ir "encendiendo" o "apagando" cada una de las entradas en los puntos marcados como d0, d1, d2, d3, etc.:
http://tams-www.informatik.uni-hamburg.de/applets/hades
_______/webdemos/10-gates/12-parity/parity8.html
Para que la demostración intercativa pueda funcionar, es necesario que la computadora en la cual se corra la simulación tenga instalada la plataforma Java (la cual se puede descargar sin costo alguno de Internet). En esta simulación, podemos comprobar cómo al ir encendiendo alternadamente una cantidad par o impar de "unos" en las entradas la salida del árbol en la terminal "o" se va "apagando" (esto lo tomamos como indicativo de un "0") o se va "encendiendo" (esto lo tomamos como indicativo de un "1") dependiendo en que el total de las entradas "encendidas" sea una cantidad impar o par (podemos invertir el sentido de la paridad en este árbol de paridad simulado con sólo "activar" la entrada en el extremo inferior izquierdo que dice "odd").
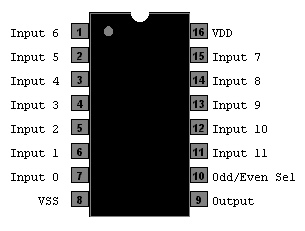
Con la misma facilidad con la cual se construye un árbol de paridad de ocho bits podemos, si queremos, construír un árbol de paridad de doce bits. Pero en este último caso, podemos ahorrarnos una buena cantidad de tiempo y esfuerzo adquiriendo comercialmente algún circuito integrado cuya función sea precisamente la misma que la de un árbol de paridad, un circuito integrado como el 4531, el cual es un árbol de paridad de 12 bits:
Este circuito integrado trabaja de la manera siguiente: Las entradas al circuito son puestas desde la terminal identificada como Input 0 hasta la terminal identificada como Input 11. En operación normal, la terminal "pin" 10 (Odd/Even Select) tiene puesto un "0". Si una cantidad par de entradas está en el estado de paridad "cero" el circuito pone un "0" en la terminal de salida identificada como Output (terminal "pin" 9), y si un número impar de entradas están en el estado de paridad "cero" entonces el circuito pone un "1" en la terminal de salida Output. Poniendo un "1" en la terminal 10 invierte el sentido de la salida Output.
En general, el árbol de paridad puede ser utilizado de dos maneras: para generar el "bit" de paridad en la palabra que será transmitida, y para detectar la paridad de la palabra recibida.
Otra técnica que ha sido ampliamente utilizada para la detección de errores es la técnica del chequeo-de-suma (sumcheck). Esta consiste en generar un número checksum, que es enviado junto con un "paquete" de datos, a partir de los mismos datos. Al recibirse el "paquete" de datos, el número checksum puede ser generado nuevamente por el receptor sumando los números que corresponden al paquete recibido, y comparado con el número checksum enviado. Si los dos checksum resultan ser diferentes, entonces se sabrá que hubo un error. Con una ligera variante, podemos hacer un poco más eficiente el proceso en la forma que se describirá a continuación.
Supóngase que vamos a enviar cuatro palabras: la palabra 00100101 (equivalente al número hexadecimal 25h), la palabra 01100010 (equivalente al número 62h), la palabra 00111111 (equivalente al número 3Fh) y la palabra 01010010 (equivalente al número 52h), junto con su checksum.
El primer paso consiste en sumar (en suma binaria) las cuatro palabras como si fueran números (pueden serlo, pero también podrían ser caracteres alfabéticos ASCII). Esto dará como resultado una palabra de nueve bits en vez de ocho, la palabra 100011000 (cuyo equivalente hexadecimal es 118h).
El siguiente paso consiste en ignorar el bit excedente resultante de la operación aritmética de "llevar", lo cual nos deja con la palabra 00011000 (cuyo equivalente hexadecimal es 18h).
El tercer paso consiste en obtener el 2-complemento (véase el Capítulo 3: El álgebra Boleana) de la palabra obtenida, el cual resulta ser 11101000 (cuyo equivalente hexadecimal es E8). Este es el byte del chequeo-de-suma que es enviado hacia afuera junto con los datos.
El receptor todo lo que tiene que hacer de su lado es sumar el checksum recibido a la suma total que obtenga del grupo recibido de cuatro bytes, sabiendo que el resultado debe ser siempre cero (recuérdese que la suma de un número al número 2-complemento derivado de ella es cero). En este caso, si sumamos 11101000 a 100011000 (la palabra de nueve bits resultante de la suma de los cuatro bytes), obtenemos 1000000000, o sea el número hexadecimal 200h, y como en el procedimiento ignoramos los bits generados por la operación aritmética de "llevar", ignoramos los dos bits "10", lo cual nos deja con la palabra 00000000, lo cual nos indica que hubo una generación de cero errores.
Otra técnica potente muy utilizada para la detección de errores es el chequeo de redundancia cíclica (Cyclic Redundancy Check ó CRC). Su modo de empleo se muestra a continuación (ampliar imagen):
Como lo muestra el diagrama, el proceso comienza con la palabra binaria a3a2a1a0 que va a ser transmitida. Se toma la palabra binaria que en este caso es de cuatro bits y se le añaden tres ceros. Hecho esto, se lleva a cabo un proceso de división binaria entre esta palabra y un divisor de cuatro bits identificado como d3d2d1d0 (tanto el transmisor como el receptor deben tener disponible en todo momento el mismo valor binario para el divisor d3d2d1d0). El resultado de este proceso aritmético se lleva a cabo en un "generador" (el cual puede ser un circuito lógico especializado o un secuenciador programable capaz de poder llevar a cabo el proceso de división), en el cual después de haberse llevado a cabo la división binaria se produce el residuo resultante de la división, identificado como r3r2r1r0, el cual es frecuentemente conocido como el CRC. Este residuo (CRC) es anexado a la palabra-dato original a3a2a1a0 formando la palabra-código a3a2a1a0r3r2r1r0. Esta palabra de siete bits es la palabra que es enviada por el "transmisor" mediante un canal de comunicaciones poco fiable, el cual puede ser una línea telefónica ruidosa. La palabra que llega al "receptor" es la palabra código de siete bits b3b2b1b0q2q1q0. Si el canal de comunicaciones fuera altamente confiable y no hubiera ocurrido ningún error durante el proceso de transmisión, la palabra código recibida b3b2b1b0q2q1q0 sería idéntica en todo respecto a la palabra código enviada a3a2a1a0r3r2r1r0. Una vez recibida la palabra código, el receptor utilizando como punto de referencia el mismo divisor d3d2d1d0 lleva a cabo el mismo proceso aritmético de división (dividiendo el mensaje entre el divisor d3d2d1d0) en un bloque "checador" obteniendo una palabra "síndrome" de tres bits s2s1s0. Si la palabra síndrome resulta estar constituída de puros "ceros", ello significa que no hubo error alguno durante el proceso de transmisión de la palabra, con lo cual se abre una compuerta dejando pasar los bits b3b2b1b0 aceptándolos como la palabra-dato original a3a2a1a0. Pero si la palabra síndrome tiene un valor diferente de cero binario, entonces la compuerta no se abrirá y por el contrario será descartada como defectuosa. Como ya se dijo, esta técnica se puede implementar con electrónica digital, con circuitos usando funciones lógicas básicas y flip-flops, como lo muestra la siguiente "tabla de secuencias" representativa del comportamiento de una "máquina CRC":
En esta "máquina" que esencialmente está hecha a base de un registro de desplazamiento del tipo entrada serial y salida serial de 5 bits (usando cinco flip-flops) con los bits desplazándose dentro de ella de derecha a izquierda en cada "pulso de reloj", se utiliza como generador del CRC la palabra binaria "1011" para obtener el CRC a partir de la palabra-dato o "mensaje" a ser transmitido que en este caso es "01100111". En la implementación de la máquina, puesto que se van a estar llevando a cabo operaciones aritméticas en el sistema binario (base-2), será inevitable en cualquier diseño de este tipo de máquina la inclusión de una función lógica que encontramos previamente tanto en la construcción del Medio-Sumador como del Medio-Substractor: el bloque OR-EXCLUSIVO o XOR.
Desde el punto de vista de la máquina (del lado del transmisor), el procesamiento se lleva a cabo bit por bit, resultando en una serie de dígitos binarios (los bits del CRC) que serán anexados posteriormente al mensaje original. El proceso comienza con todos los flip-flops de la máquina puestos en "ceros", tras lo cual el mensaje va siendo desplazado hacia la izquierda siendo introducido bit por bit dentro del registro de desplazamiento (esto está simbolizado con una letra "M" que tiene anexada una flecha a la misma apuntando hacia la izquierda) seguido de cuatro ceros (simbolizado cada uno de ellos con un número "0" también con una flecha anexada apuntando hacia la izquierda), de modo tal que entra el mensaje seguido de cuatro ceros. Obsérvese que cuando el bit más significativo (el bit más a la izquierda) es "1" (esta es la situación que tenemos en el séptimo renglón de la tabla de secuencias, con el "1" de color rojo sobre un fondo negro) se lleva a cabo entonces la operación de OR-EXCLUSIVO con el "generador" que en este ejemplo es la palabra "10011". Esto se repite cada vez que el bit más significativo es "1", lo cual ocurre tres veces (en el séptimo, en el noveno y en el 13avo renglón). Los cuatro bits de orden más bajo, resultado final del proceso de división aritmética en el sistema binario (base-2), son entonces el CRC que será anexado a la palabra-dato original justo antes de llevarse a cabo la transmisión del mensaje, el cual en este caso es "0110" (en el renglón inferior de la tabla de secuencias) descartando el "0" que está en la posición del bit más significativo. Para este proceso hemos supuesto que el generador es una palabra no de cuatro bits sino de cinco; sin embargo el bit más significativo en el generador no es realmente de interés y por lo tanto no se le toma en cuenta, porque en primer lugar el bit más significativo en el generador siempre es "1", y cuando el bit más significativo (más a la izquierda) dentro del registro se vuelve "1", el generador es sometido a una operación de OR-EXCLUSIVO contra los contenidos del registro, "limpiando" el bit más significativo. Por lo tanto, el bit más significativo no necesita ser transmitido.
También la palabra código resultante (la palabra-dato más la secuencia CRC), al pasar por el "hardware" CRC, deja "limpio" el registro. Esto se puede visualizar mejor alimentando la secuencia "01101110110" (consistente en la palabra-dato "0110111" con el CRC "0110" anexado) adentro del registro de transferencia siguiendo las reglas indicadas. El contenido del registro terminará siendo "cero" al final.
Puesto que a las velocidades actuales de procesamiento que actualmente andan arriba del orden de 1 Gigabit por segundo es muy difícil diseñar circuitos lógicos CRC que puedan hacer todas sus operaciones a esta velocidad, los ingenieros frecuentemente diseñan los circuitos CRC para procesar varios bits a la vez.
Para que el chequeo de redundancia cíclica pueda trabajar, matemáticamente hablando, es necesario que la palabra que va a ser transmitida sea considerada en nuestros análisis como un polinomio. A modo de ejemplo, para el siguiente dato binario de 16 bits a ser transmitido:
0010 0110 1111 0000 (26F0h, hexadecimal)
el polinomio formado directamente a partir de cada uno de los bits es el siguiente (obsérvese la correspondencia entre cada uno de los bits de la palabra y cada uno de los coeficientes "unos" y "ceros" del polinomio):
M(X) = 0 + 0X1 + 1X2 + 0X3 + 0X4 + 1X5 + 1X6 + 0X7 + 1X8 + 1X9 + 1X10 + 1X11 + 0X12 + 0X13 + 0X14 + 0X15
M(X) = 1X2 + 1X5 + 1X6 + 1X8 + 1X9 + 1X10 + 1X11
Tras esto, y tomando n como la cantidad de bits de que está formada la palabra que será transmitida (n=16 en este ejemplo) se lleva a cabo un proceso de división entre este polinomio M(X) y un polinomio generador G(X) que tiene propiedades especiales:
M(X)Xn/G(X) = Q(X) + R(X)
en donde Q(X) es el cociente de la división y R(X) es el residuo resultante de la misma. Es precisamente este residuo binario R(X) lo que es anexado a la palabra-dato que será transmitida. A continuación tenemos detallado el proceso de división para el ejemplo que estamos utilizando, en donde nuestro polinomio generador G(X) es un polinomio utilizado con mucha frecuencia, el polinomio G(X)=X16+X15+X2+1 (ampliar imagen):
En el receptor,después del cálculo CRC de su lado, el residuo R(X) debe ser cero para que la palabra pueda ser considerada como transmitida sin error alguno.
Una cosa que hay que tener presente es que, al nivel de la máquina digital, la cual trabaja en el sistema binario, no es necesario proporcionarle a la máquina una "calculadora" para que pueda llevar a cabo el proceso de división binaria; ya al igual que en el caso de la multiplicación binaria, la cual se puede llevar a cabo con un registro de transferencia serial y simples adiciones, la división binaria se puede llevar a cabo también con un registro de transferencia serial y simples substracciones. No hay que olvidar que este proceso, que a nosotros nos puede parecer muy laborioso, al final del día no será llevado a cabo por nosotros sino por la misma máquina en donde esté instalado ya sea el productor (en el transmisor) o el verificador (en el receptor) de la redundancia cíclica. Sin embargo, considerando que en un proceso de transmisión de datos de un archivo sumamente grande (con un tamaño en el orden de los megabytes) estos procesos aritméticos repetidos una y otra vez miles y miles de veces invariablemente tendrán un impacto en la disminución de la velocidad de la transmisión de los datos, esto ciertamente tiene que ser considerado como un factor en cualquier diseño que tenga que ver con las áreas de aplicación de la técnica CRC.
A continuación se muestra un cálculo simplificado, muy a la manera de como los matemáticos efectúan el proceso algebraico de división sintética, prescindiendo de las "equis" (que en realidad sólo están haciendo "bulto" aquí), en donde el polinomio M(X) es obtenido de la palabra 11100110 y en donde el polinomio generador G(X) es el que está dado por la palabra 11001, obteniéndose el residuo 0110 que es lo que será anexado a la palabra-dato original a ser enviada (ampliar imagen):
Además de la capacidad para poder detectar errores (error detection), es posible darle a los circuitos lógicos también la capacidad para poder corregir errores (error correction). Esto requiere, desde luego, agregar información redundante adicional a una palabra que permita localizar la posición exacta del bit que está produciendo un error de paridad, ya que el error de paridad por sí solo en una palabra no nos indica cuál de todos los bits es el bit incorrecto. Un esquema utilizado en algunos diseños consiste en tomar varias palabras binarias "en bloque", digamos unas ocho palabras, de modo tal de que además de que cada palabra (representada por un renglón) tenga un bit de paridad, al final de cada bloque de ocho palabras haya una palabra completa "extra" redundante, la cual consistirá de ocho bits de paridad, uno para cada columna. De esta manera, si en lugar de un "1" tenemos un "0" en una palabra, además de la paridad incorrecta que nos permite identificar cuál de las ocho palabras viene con un error tenemos la paridad incorrecta del bloque que nos permite identificar cuál bit de esas ocho palabras es el que está en el error.
Seleccionando una paridad impar como denotando una palabra correcta sin errores y también como denotando una bloque completo de palabras correcto sin errores, a continuación tenemos un bloque que carece errores en la transmisión y en la recepción (cada renglón representa una palabra binaria diferente):
Puesto que todas las palabras binarias del bloque tienen la paridad correcta (impar), no hay errores en la transmisión de este bloque. En cambio, en el siguiente bloque, tenemos una palabra con tres errores:
En este caso, la penúltima palabra (en el penúltimo renglón) viene con tres errores. Su paridad par nos dice que tiene por lo menos un error. Además, la paridad en las columnas nos permite detectar la presencia de tres errores en la palabra e identificar la localización precisa de los tres bits erróneos: están en el cuarto, el quinto, y el séptimo bit de la penúltima palabra binaria.
La localización exacta de un bit erróneo nos permite diseñar una máquina que sea capaz no sólo de detectar estos tres errores sino también corregirlos. Y aunque a nosotros como humanos el proceso nos pueda parecer dificultoso, es relativamente fácil enseñarle a una máquina a corregir este tipo de errores, lo cual haría con rapidez electrónica. Existen procedimientos matemáticos muy específicos para agregar bits redundantes que permitan no sólo la detección de errores sino la corrección de los mismos, conocidos como códigos correctores de errores (error correcting codes ó ECC). Uno de ellos es el código Hamming. Considérese una palabra binaria consistente de únicamente cuatro bits de datos que será transmitida como una palabra-código (codeword) con la adición de tres bits de control de error. Esto sería llamado un código (7,4). Los tres bits agregados son tres bits de paridad par, en donde la paridad de cada uno es calculada en distintos subconjuntos del mensaje de la manera que se muestra abajo:
La razón teórica para este tipo de arreglo es que los tres bits de paridad (1,2,4) están relacionados con los cuatro bits de datos (3,5,6,7) de la manera que se muestra a continuación:
En este diagrama cada círculo corresponde a un bit de paridad, y define los cuatro bits que contribuyen al cálculo del bit de paridad. Por ejemplo, el bit de datos 3 contribuye a los bits de paridad 1 y 2. Cada círculo (bit de paridad) abarca un total de cuatro bits (tres bits de datos y un bit de paridad), y cada círculo por lo tanto debe tener una paridad par. Dados cuatro bits de datos cualesquiera en cualquier combinación de "unos" y "ceros", los tres bits de paridad pueden ser seleccionados fácilmente para cumplir con esta condición, y como de costumbre le dejaremos la carga de este trabajo a la máquina.
Se puede observar en el diagrama que cambiando cualesquier bit numerado del 1 al 7 afecta de modo único los tres bits de paridad. Alterando el bit 7 afecta todos los tres bits de paridad, mientras que un error en el bit 6 afecta únicamente a los bits de paridad 2 y4, mientras que un error en un bit de paridad (lo cual también puede ocurrir durante el proceso de transmisión) afecta únicamente a ese bit de paridad. La localización de cualquier error individual en un bit está determinada unívocamente después de checarse los tres círculos de paridad.
Con este esquema de detección y corrección de errores, la palabra binaria (datos) "1101" sería enviada como la palabra-código "1100110" con la adición de los tres bits de paridad, puesto que:
Cuando estos siete "unos" y "ceros" son introducidos en los círculos de paridad, se puede confirmar que la selección de los tres bits de paridad asegurará que la paridad dentro de cada círculo será par, como se muestra aquí:
Se puede observar aquí que si ocurre un error en cualesquiera de los siete bits, ese error afectará distintas combinaciones de los tres bits de paridad dependiendo de la posición del bit que llega con error. Supóngase por ejemplo que se envía el mensaje "1100110" y que ocurre un error en un solo bit tal que se recibe la palabra-código "1110110":
El error en el mensaje, en el bit 5, puede ser corregido examinando cuáles de los tres bits de paridad fueron afectados por el bit defectuoso:
En el segundo renglón en el cual se utiliza el bit de paridad 1 y el cual tiene un valor de un "0", la cantidad total de "unos" es un número impar, 3, lo cual indica que ha ocurrido un error de acuerdo con el criterio de que bajo la paridad par si se produce un "1" en lugar de un "0" ello apunta hacia la presencia de un error. En el tercer renglón, en el cual se utiliza el bit de paridad 2 y el cual tiene un valor de un "1", la cantidad total de "unos" es un número par, 4, lo cual indica que aquí no hay indicación de error alguno según el criterio de que bajo la paridad par se debe producir un "0" como consecuencia de un número par de "unos". Y en el cuarto renglón, en el cual se utiliza el bit de paridad 4 y el cual tiene un valor de "0", la cantidad total de "unos" es un número impar, 3, lo cual indica que ha ocurrido un error. Los bits de paridad así como la palabra código original permiten determinar la posición del "bit" que llegó defectuoso, o sea el bit 5 que llegó como un "1" en vez de haber llegado como el "0" que debía haber sido. El examen de los círculos de paridad confirma que cualquier bit defectuoso puede ser corregido de esta manera. El código Hamming tiene pues las siguientes características (1) La capacidad para detectar en una palabra transmitida dos bits en el error, lo cual supone que no se intentará llevar a cabo una corrección del error, (2) La corrección de bits individuales de error, o sea un error de un bit en una palabra transmitida, y (3) Un costo de tres bits que se tienen que añadir a un mensaje de 4 bits. Esto último puede parecer oneroso. Sin embargo, la capacidad para poder corregir errores viene a un costo que es menor que el tener que enviar de nuevo el mensaje completo, y tómese en cuenta que el envío del mensaje por partida doble no logra ninguna corrección de error.
Al hablar sobre el tema de la detección y corrección de errores, es frecuente manejar el concepto de la distancia entre dos palabras binarias. Aunque a este concepto casi siempre se le dá en los libros de texto una definición formal que también casi siempre resulta críptica, aquí daremos una definición naïve del concepto: es simplemente la cantidad de bits que tienen que ser cambiados para igualar una palabra binaria con otra. Así, la distancia entre las palabras 10011000 y 00011000 es 1 porque basta con cambiar el primer bit de cualquiera de las dos palabras para igualar una con otra. Entre más "alejada" esté una palabra binaria de la otra, tanto mayor será la cantidad de bits que tengamos que cambiar para igualar una de ellas con la otra. El código Hamming permite la corrección de errores porque la distancia mínima entre dos palabras código es 3. En la figura de abajo, dos palabras código en ocho posibles palabras código de tres bits están acomodadas para tener una distancia de 3 entre ellas. Se requieren tres cambios de bits (errores) para moverse de una palabra código 000 válida a los siguientes 111. Si la palabra código 000 es transmitida y ocurre un error en un bit, la palabra recibida necesariamente será una del conjunto {001, 010, 100}, cualquiera de las cuales puede ser identificada fácilmente como una palabra código inválida, y la cual podría haber sido únicamente la palabra código 000 antes de la transmisión.
El código Hamming define esencialmente 16 palabras código válidas dentro de todas las 128 palabras código posibles de 7 bits. Estas 16 palabras están acomodadas de modo tal que la distancia mínima entre dos palabras cualesquiera sea 3. Estas palabras código son mostradas en la siguiente tabla:
Se puede verificar que la distancia de cualquier palabra código M={0,1,2,...,E,F} de esta tabla a cualquier otra palabra código N es de por lo menos 3. A continuación tenemos unos ejemplos en donde medimos la distancia de la palabra código 3 hacia otras palabras código para confirmar esta aseveración:
La distancia es 4 entre 3 = 0011110 y 0 = 0000000Continuando con el chequeo de la distancia entre la palabra código 3 y todas las demás palabras código restantes, podemos concluír que la palabra código 3 está situada a una distancia de por lo menos 3 de todas las demás palabras código.
La distancia es 3 entre 3 = 0011110 y 1 = 0000111
La distancia es 3 entre 3 = 0011110 y 2 = 0011001
La distancia es 4 entre 3 = 0011110 y D = 1100110
La distancia es 4 entre 3 = 0011110 y E = 1111000
La distancia es 3 entre 3 = 0011110 y F = 1111111
Con la misma facilidad con la que construímos el código (7,4) podemos construír otros códigos Hamming, por ejemplo el código (8,4).
Con un poco de análisis matemático podemos obtener una fórmula que nos indica en forma precisa cuántos bits redundantes adicionales se requieren para garantizar la detección y corrección de un error con el código Hamming. La fórmula es Ham(2n, 2n-n-1). Por ejemplo, si n=7, tenemos entonces Ham(128,120), lo cual nos dice que para cada 120 bits de datos únicamente se requieren ocho bits extra redundantes para protegernos en contra de un error dándonos la capacidad no sólo para poder detectarlo sino también para poder corregirlo. Y cuando n=20, entonces obtenemos Ham(1048576,1048555), lo cual nos dice que se requieren únicamente 21 bits para codificar más de un millón de bits y aún garantizarnos una protección en contra de un error.
Como una cortesía de la Universidad de Hamburgo en Alemania, se encuentra disponible en Internet en el siguiente domicilio un programa interactivo que permite al estudiante el poder "experimentar" con un envío y recepción de un mensaje binario utilizando la adición de bits de paridad y el código Hamming para poder detectar la presencia de errores así como la determinación del bit defectuoso. El programa interactivo puede ser accesado en el siguiente domicilio:
http://tams-www.informatik.uni-hamburg.de/applets/hades
_______/webdemos/10-gates/50-hamming/hamming.html
Esta simulación trabaja con un circuito que utiliza un código Hamming de 4 bits para detección y corrección de errores. Los cuatro interruptores a la izquierda se utilizan para fijar el valor de 4 bits para el codificador, el cual calcula el valor requerido por cada uno de los tres bits de paridad que serán transmitidos junto con los cuatro bits de datos como una palabra código. Los siete interruptores (Set channel faults) y las compuertas OR-EXCLUSIVO en la parte media del circuito permiten introducir manualmente "fallas" en el mensaje transmitido. Si todos los interruptores están "apagados", el mensaje es transmitido en forma normal, pero si se "enciende" uno de los interruptores entonces la compuerta OR-EXCLUSIVO asociada al interruptor invierte el bit del dato correspondiente (conviertiendo un "0" en un "1" ó un "1" en un "0"), lo cual equivale a que ese bit haya sido transmitido como error. El bloque decodificador a la derecha del circuito toma los siete bits del mensaje e intenta reconstruír con los siete bits la información original, o sea los cuatro bits del mensaje original. Los creadores del programa interactivo recomiendan tener todos los siete interruptores "apagados" experimentando con el envío de algunos mensajes; seleccionando algunos valores de entrada para el codificador con los interruptores a la izquierda para así poder observar los bits de paridad que se generan así como el modo de funcionamiento del decodificador. Tras esto, recomiendan "jugar" con algunos de los interruptores para introducir manualmente "fallas" individuales en el mensaje transmitido, observando la operación del decodificador. Y finalmente, invitan al experimentador a descubrir qué es lo que ocurre cuando se activa más de un "interruptor generador de error".