Por último, vamos a estudiar el concepto del
diagrama de tiempos, el cual siempre se lee
de izquierda a derecha.
Supóngase que con el transcurso del tiempo, un circuito lógico produce la siguiente salida en tiempos igualmente espaciados t
n:
En el transcurso del tiempo de t
1 a t
2, la salida es
1. En el transcurso del tiempo t
2 a t
3, la salida es
0. Podemos ver cómo en el transcurso del tiempo t
1 a t
3 se habrá formado la palabra:
10
En el transcurso del tiempo t
3 a t
4 la salida es
1. Y en el transcurso del tiempo t
4 a t
5 la salida también es
1. Vemos que en el transcurso del tiempo t
1 a t
5 se habrá formado la palabra:
1011
Así, desde el inicio del tiempo t
1 hasta el final del tiempo t
10 se habrá formado la palabra:
101101001
En general, dado un diagrama de tiempos podemos obtener a partir del mismo la palabra binaria que éste genera
siempre y cuando estemos seguros del espaciamiento de tiempos entre un "bit" y el que le sigue. La división precisa del tiempo es crucial para poder fijar y distinguir en forma correcta los "unos" y los "ceros". En el caso que acabamos de ver, si la división del tiempo cronometrada en cierto sistema digital fuera el doble de lo que acabamos de ver, entonces en lugar de la palabra
1011 generada desde el comienzo de t
1 hasta el final de t
5 podríamos muy bien haber tenido la palabra
11001111. Y si fuera el triple, entonces la palabra debería haber sido
111000111111. Este detalle se vuelve mucho más importante cuando la palabra binaria que está siendo enviada o procesada es una palabra que consta de puros "unos" (como
11111111) o de puros "ceros" (como
00000000) porque en tal caso la misma palabra no nos proporciona absolutamente ninguna pista sobre cuántos "bits" la forman.
Así como podemos obtener de un diagrama de tiempos la palabra binaria mostrada por dicho diagrama, de la misma manera dada una palabra binaria podemos obtener a partir de la misma el diagrama de tiempos que la produce. Por ejemplo, el diagrama de tiempos de la palabra:
11011101
será como se muestra a continuación:
Con mucha frecuencia en el estudio y análisis de sistemas digitales, los diagramas de tiempo se presentan como diagramas de tiempos
múltiples,
sincronizados. Esto quiere decir que en lugar de un solo diagrama podemos tener dos, tres, o más diagramas, alineados uno encima del otro de tal modo que sus tiempos se correspondan mutuamente. A continuación tenemos un diagrama de tiempos múltiple de un circuito digital que posee
cuatro salidas en lugar de una sola, designadas como
Q0,
Q1,
Q2 y
Q3:
Aunque a primera vista no lo parezca, el circuito que produce este diagrama de tiempos múltiple está llevando a cabo una labor muy importante. Podemos entender mejor lo que está sucediendo si acomodamos las salidas de modo tal que se forme la palabra binaria:
Q3Q2Q1Q0
Veamos ahora lo que va sucediendo conforme el tiempo va transcurriendo
de izquierda a derecha, veamos las palabras binarias que se van formando empezando por la primera:
Q3Q2Q1Q0 = 0000
Q3Q2Q1Q0 = 0001
Q3Q2Q1Q0 = 0010
Q3Q2Q1Q0 = 0011
Q3Q2Q1Q0 = 0100
∙ ∙ ∙
Posiblemente a estas alturas ya sea obvio lo que está realizando el circuito lógico que produce este diagrama de tiempos. Es un
contador binario de conteo ascendente. Está contando
hacia arriba en el lenguaje propio de las máquinas electrónicas, en el lenguaje binario de "unos" y "ceros".
El que sigue es un diagrama de tiempos múltiple producido por un
contador binario de conteo descendente, o sea un contador binario que está contando
hacia abajo, como si fuese una cuenta regresiva:
El lector observador se habrá dado cuenta ya de que el circuito lógico que produce este diagrama de tiempos tiene salidas
complementadas:
Q0, Q1, Q2, y Q3. De hecho, si comparamos este diagrama de tiempos con el anterior, no tardaremos en darnos cuenta de que podemos obtener un contador binario de conteo descendente (
hacia abajo) de un contador binario de conteo ascendente (
hacia arriba)
con el solo hecho de conectar unos inversores NOT a las salidas Q0,
Q1,
Q2 y Q3 del contador binario de conteo ascendente.
A continuación, se muestran en acción animada varios diagramas de tiempos para varias de las funciones lógicas básicas que hemos estudiado hasta ahora (
ampliar imagen para poder ver los efectos especiales de animación):
Veamos primero los diagramas de tiempos que corresponden al bloque AND que aparecen en el primer renglón en la columna de la izquierda. Al comenzar la animación, las dos entradas al bloque AND tienen un "
0" lógico, con lo cual la salida del AND también tiene un valor de "
0". Al transcurrir el tiempo, la entrada superior cambia de "
0" a "
1". Pero como se trata de un bloque AND que requiere que las dos entradas sean "
1" para producir una salida de "
1", el diagrama de tiempos que corresponde a la salida permanece en "
0". Poco después, la entrada inferior también es puesta en "
1", con lo cual ambas entradas ya son "
1". Esto provoca que en el diagrama de tiempos la salida del AND cambie de inmediato a "
1", y este cambio es confirmado al encenderse el diodo emisor de luz LED al ocurrir el cambio. Tras esto, al caer el valor en la entrada superior de "
1" a "
0", la salida del AND también se desploma nuevamente a "
0", lo cual es confirmado por el diagrama de tiempos a la salida del AND y por el indicador luminoso.
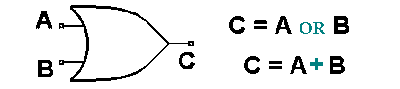
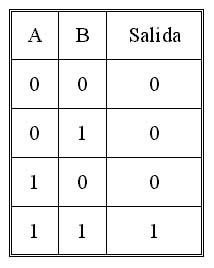
En la misma columna, en el tercer renglón, tenemos un bloque OR, el cual dará una salida de "
1" cuando cualquiera de las dos entradas sea "
1". Siguiendo la acción en el diagrama de tiempos como lo hicimos en el caso del bloque AND, podemos verificar lo que nos están diciendo los diagramas de tiempos para el OR en su conjunto. En el segundo renglón de la misma columna tenemos un bloque NAND y en el cuarto renglón tenemos un bloque NOR con sus respectivos diagramas de tiempo.
Existe equipo de laboratorio, un poco caro por cierto, utilizado precisamente para obtener los diagramas de tiempos de circuitos como los que hemos estado estudiando, conocidos como analizadores lógicos, de los cuales tenemos uno a continuación:
En el siguiente diagrama de tiempos, tenemos ilustrado el comportamiento de un bloque NAND con tres terminales de entrada
A,
B y
C, y una salida designada como
Y:
La forma de leer este diagrama de tiempos es la siguiente,
procediendo siempre de izquierda a derecha. Al principio, las tres entradas
A,
B y
C tienen un valor lógico de
0, con lo cual la salida
Y es
1. Al irnos moviendo de izquierda a derecha, vemos que la entrada
A es llevada de
0 a
1, aunque esto no produce ningún efecto en la salida
Y por tratarse de un NAND. Tras esto, y con la entrada
A mantenida con un valor de
1, la entrada
B es también llevada hasta un
1 lógico, pero de nueva cuenta, no sucede nada a la salida por tratarse de un NAND. Tras esto, la entrada
C es también llevada hasta un
1 lógico, con lo cual las tres entradas del NAND tienen ya un valor de
1. Esto produce un transición en el valor de la salida
Y de
1 a
0, lo cual está resaltado con la línea flechada. Por último, la entrada
A es llevada nuevamente al valor de
0 que tenía originalmente, lo cual produce un cambio
casi inmediato en la salida
Y del NAND que lo lleva de
0 a
1. Esto concluye la lectura del diagrama de tiempos.
Obsérvese que en el último párrafo usamos la palabra
casi.
Los diagramas de tiempos que se acaban de describir están modelados en base al diagrama de tiempos
ideal, en el cual supuestamente una señal asciende
instantáneamente de
0 a
1 ó desciende
instantáneamente de
1 a
0, lo que requiere que un voltaje (digamos de +5 volts) suba instantáneamente a un valor desde cero volts hasta dicho valor de +5 volts sin retardo alguno de tiempo, o viceversa. En circuitos lógicos construídos con componentes reales tales como semiconductores, resistencias y capacitores, esto simple y sencillamente no es posible, porque por principio de cuentas ninguna señal se puede propagar a una velocidad mayor que la velocidad de la luz, y mucho antes de llegar a ese límite entran en acción otros fenómenos que imponen restricciones en cuanto a la rapidez con la cual se puede llevar a cabo una transición de
0 a
1 ó de
1 a
0. Los siguientes dos diagramas de tiempo muestran lo que sucede con una señal real, además de mostrarnos una diferencia muy común en la representación de los dos principales tipos de señales: (a) una señal que representa un
pulso, y (b) una señal que representa un
dato binario:
En el primer diagrama (a), tenemos el diagrama de un pulso real, el cual no sube instantáneamente de un valor de "
0" lógico (que en la escala vertical a la izquierda vendría representando un voltaje de cero volts) hasta un valor de "
1" lógico (que en la escala vertical a la izquierda vendría representando un voltaje de algo así como +3 volts o +5 volts dependiendo del tipo de componentes usados en el circuito). La señal tarda en subir desde "
0" hasta "
1" un tiempo
Tr conocido usualmente en la literatura técnica como el
tiempo de ascenso (
rise time). Y cuando la señal desciende nuevamente de "
1" a "
0", la señal tarda un tiempo
Tf en caer conocido en la literatura técnica como el
tiempo de caída (
fall time). Una señal como la que se muestra en este diagrama, si es repetitiva, repitiéndose en forma idéntica una y otra vez, podría representar algo así como los pulsos de una
señal de reloj utilizada para poner en marcha unos circuitos lógicos conocidos como
circuitos secuenciales que serán estudiados en capítulos posteriores de este libro. En tal caso, el intervalo de tiempo entre un pulso y el que le sigue es conocido como el
período de tiempo T de la señal de reloj, con una duración desde
t1 hasta
t3. La
recíproca f del período
T, o sea
f=1/T, es la
frecuencia de la señal. Cualquiera que haya comprado alguna vez una computadora personal de escritorio desembolsando dinero de su propio bolsillo tal vez sin darse cuenta ya está familiarizado con este concepto, porque esta es precisamente la rapidez con la cual puede trabajar la computadora, y como es bien sabido las computadoras más rápidas (y las más apetecidas) son precisamente las de mayor precio. De este modo, cuando hablamos de una computadora de 500 MHz, estamos hablando realmente de una computadora con una velocidad, o mejor dicho, con una frecuencia de los pulsos de su
reloj maestro interno, de 500 millones de ciclos por segundo. Y si la velocidad es de 2 GHz, el reloj maestro interno de la computadora estará ciclando a una frecuencia de 2 millones de ciclos por segundo.
En el segundo diagrama (b), tenemos un diagrama de tiempos para la representación de una señal binaria que puede causar cierta confusión en los neófitos que no están acostumbrados a leerla, porque tenemos dos datos
sobrepuestos uno encima del otro. Este diagrama puede interpretarse como
una sola señal con dos alternativas posibles en donde la línea
roja representa la alternativa de que la señal vaya de "
0" a "
1" en un tiempo de ascenso
tr, y en donde la línea
azul representa alternativa de que la señal esté yendo de "
1" a "
0" y en cuyo caso estamos hablando de un tiempo de caída
tf. De este modo, la línea roja representa una señal que asciende brevemente de "
0" a "
1" y tras esto vuelve a caer a "
0", mientras que la línea azul representa una señal que cae brevemente de "
1" a "
0" y tras esto vuelve a subir nuevamente de "
0" a "
1". Estos son los dos comportamientos posibles y aceptables que puede tener la señal binaria mixta mostrada por el diagrama. Sin embargo, esta señal binaria mixta también tiene otro tipo de interpretación en la cual no la interpretamos como una sola señal sino como
varias señales que están siendo enviadas
simultáneamente. Bajo este modo de interpretación, un diagrama de tiempo con dos líneas "cruzadas" en el cual al inicio de un ciclo de operación una de ellas va de "
0" a "
1" mientras que la otra va de "
1" a "
0", volviendo ambas señales a sus valores originales al finalizar el ciclo, en realidad está representando no una sola línea sino
varias líneas paralelas que llevan información
en forma simultánea (como el domicilio
A6A5A4A3A2A1A0), algunas de las cuales pueden tener un valor lógico de "
0" y otras de las cuales pueden tener un valor lógico de "
1" al mismo tiempo.
Como otro ejemplo del diagrama de tiempos mixtos como el que acabamos de ver, es posible que el lector se encuentre en la literatura técnica algo como lo siguiente:
Un diagrama de tiempos de este tipo es una cosa que encontraríamos al estar estudiando algo así como los microprocesadores (hay más detalles sobre esto en el
Suplemento # 2 de este libro, titulado
El Microprocesador). Este diagrama de tiempos nos dice que se están generando una serie de pulsos de reloj (desde una terminal llamada
clock), y que tras un primer pulso de reloj podemos colocar información binaria en un conjunto de terminales designadas domicilio (
address). De nueva cuenta, la línea que se divide en dos puede parecer desconcertante. Sin embargo, no se trata de algún voltaje "intermedio" entre el "
0" y el "
1" (lo cual, dicho sea de paso, no está permitido dentro de la lógica binaria), lo que nos dice el diagrama es que en este tiempo
válido (
valid) con duración de dos pulsos de "reloj" (
clock) podemos poner información que puede consistir tanto de "unos" (
1) como de "ceros" (
0) especificando un domicilio (
address), tras lo cual podemos tomar o depositar a lo largo de cuatro ciclos de "reloj"
datos paralelos en un conjunto de terminales designadas datos (
data) que puede consistir tanto de "unos" como de "ceros".
Como se verá en la sección de problemas resueltos correspondientes a este capítulo, el álgebra Boleana es crucial para poder diseñar los circuitos digitales que se encargarán de llevar a cabo la suma binaria (no la suma Boleana) de dos números binarios distintos A y B. Los bloques fundamentales que servirán como punto de partida para esto son el
Medio Sumador (
Half Adder), el
Sumador Completo (
Full Adder), el
Medio-Substractor (
Half Subractor) y el Substractor Completo (
Full Substractor). Estos bloques fundamentales nos permiten llevar a cabo operaciones aritméticas, y como los bloques básicos son idénticos, el uso de una cantidad mayor de bloques iguales nos permite aumentar enormemente la precisión numérica de la aritmética que podemos llevar a cabo, esa increíble precisión a la cual las computadoras digitales le deben su fama. Un detalle que había quedado pendiente desde que nos introducimos a la numeración binaria fue el problema de llevar a cabo operaciones aritméticas no sólo con números binarios positivos sino también con números binarios
negativos, cuya discusión se había postpuesto hasta ahora porque en aquél capítulo introductorio no contábamos con las tres funciones lógicas básicas y mucho menos con el álgebra Boleana de la cual ya disponemos ahora para el diseño de circuitos lógicos, razón por la cual ha llegado el momento de retomar el tema.
En el primer capítulo de este libro, al introducir la numeración binaria, se describió una convención universal bajo la cual los números binarios negativos son distinguidos de los positivos con un "bit" puesto al principio del número binario, en donde el "
0" representa un "+" y el "
1" representa un "-". También se señaló allí que si se intenta sumar dos números binarios de signos distintos bajo esta convención el resultado aritmético será incorrecto. Para operaciones aritméticas binarias con signos distintos se acostumbra recurrir a una representación alterna basada en el
uno-complemento (en inglés:
one's complement ó
1's complement). Se trata de la representación conocida como el
dos-complemento (en inglés:
two's complement ó
2's complement).
Antes de entrar a fondo en la cuestión sobre la suma de números positivos y negativos en el sistema binario, trataremos aquí brevemente acerca de cómo trabaja un método conocido como el
9-complemento en el sistema decimal. Este método nos permite llevar a cabo la operación aritmética de resta (substracción) entre dos números, o lo que es lo mismo, la suma de un número positivo a un número negativo (el número que está siendo restado). En el sistema decimal, el
9-complemento de un número se obtiene reemplazando cada dígito del número por nueve menos el dígito. De este modo, el 9-complemento de 147 es 852 y el complemento de 605 es 394. Bajo la técnica del 9-complemento, para sumar 605 a -147 el procedimiento sería el siguiente:
Como puede verse, se obtiene primero el complemento del número cuyo signo sea negativo, se suman los números, y tras esto se suma el 1 previamente obtenido de la operación de "Llevar" a lo que tenemos, para así lograr el resultado final, que en este caso es +458. De este modo, la operación aritmética de la resta queda reducida a una operación de suma aritmética. En lugar de restar como lo haríamos en un cálculo hecho a mano, cambiamos 147 por su complemento procediendo a sumar. El sobreflujo es llevado a la columna de las "unidades" y sumado, obteniendo el resultado correcto de la operación. A continuación se llevará a cabo la misma operación, pero invirtiendo los signos:
Aquí también tomamos el complemento del número negativo. En este caso no hay sobreflujo, y el procedimiento final es algo diferente. La suma resultante del número positivo y el complemento del otro número es simplemente complementada, y al resultado se le asigna un número negativo.
La justificación del por qué este método siempre trabaja nos llevaría a una discusión sobre el tema de los anillos matemáticos y las clases de equivalencia, lo cual nos desviaría de nuestro objetivo central sin añadir más claridad a la técnica. Nos basta con saber que este método nunca falla porque tiene una justificación teórica sólida.
Así como en la numeración decimal se tiene al método del 9-complemento para poder sumar un número positivo y un número negativo, también en otros sistemas numéricos existe un procedimiento similar apoyado por las mismas razones matemáticas teóricas. En nuestro caso, estamos interesados en la aplicación de la técnica al sistema binario, al lenguaje de "unos" y "ceros" que es el que entienden las máquinas. Dicho esto, todo lo anterior mejor preparados para definir lo que es el "uno complemento" en el sistema binario. Esta representación tomamos simplemente el inverso lógico del número binario, o lo que es lo mismo,
su complemento (de aquí deriva la designación). Así, el
uno-complemento del número binario
00000010 (equivalente al número decimal 2) es
11111101.
Bajo la representación del "dos complemento", tomamos primero el
1-complemento del número en la forma que ya se señaló, simplemente invirtiéndolo lógicamente. Tras esto, se le suma 1. Esto resulta en la codificación del número en
2-complemento. Es importante recalcar que al tomar un número positivo el procedimiento de representarlo como 2-complemento lo convierte automáticamente en un número negativo.
Veamos a continuación un ejemplo de cómo podemos obtener la representación del número -9 bajo el esquema del
2-complemento usando una palabra binaria de cuatro "bits" (un
nibble) con el primer bit reservado para el signo del número y los tres bits restantes reservados para la magnitud del número. Empezamos con el equivalente binario del número decimal "9", que es "
01001". Le aplicamos ahora el proceso de inversión lógica para obtener el 1-complemento, que es "
10110". Por último le sumamos 1 y obtenemos "
10111". Este es el equivalente,
en 2-complemento, del número
negativo -9.
Dado un número en
2-complemento, podemos convertirlo a su forma negativa decimal sumando las "potencias de 2" de los bits "1", pero dándole un "peso" negativo al bit (del signo) más significativo que va a la izquierda. Por ejemplo:
111110112 = - 128 + 64 + 32 + 16 + 8 + 0 + 2 + 1
111110112 = - 5
o por ejemplo:
100010102 = -128 + 0 + 0 + 0 + 8 + 0 + 2 + 0
100010102 =10001010 = -118
Para que estas conversiones queden claras, recurriremos a otro ejemplo sencillo convirtiendo primero el número 13 en base decimal a su negativo usando su representación como 2-complemento, y después tomando este resultado obtendremos el número negativo expresado en sistema decimal. El número 13 en formato binario es
00001101. Si invertimos los bits obtenemos como
1-complemento 11110010. Ahora le sumamos
1, y obtenemos el
2-complemento 11110011. Podemos checar la respuesta convirtiendo este número 2-complemento a su equivalente decimal:
11110011 = -128 + 64 + 32 + 16 + 0 + 0 + 2 + 1
11110011 = -13
Cabe notar que el 2-complemento de cero es cero: invirtiéndolo primero nos dá una cadena de "unos", y al sumarle "1" esto cambia todos los "unos" nuevamente a ceros. Al hacer esta operación,
el sobreflujo es simplemente ignorado.
A continuación tenemos una tabla que nos muestra el equivalente de varios enteros positivos y negativos decimales representados en la segunda columna bajo el esquema "
signo magnitud" (el primer bit es usado para el signo y los tres bits restantes para la magnitud) y representados en la tercera columna bajo el esquema
2-complemento:
La misma información tal vez sea más fácil de visualizar y recordar con el siguiente "círculo binario":
Ahora llevaremos a cabo la suma de dos números de signos distintos, +2 y -3, bajo la representación del 2-complemento, usando una extensión de un byte (ocho bits). Puesto que el único número que lleva un signo negativo es el 3, tomamos el 3 cuyo equivalente binario (positivo) es
0011, lo invertimos lógicamente para obtener el 1-complemento, que es
1100, y le sumamos
1 con lo cual obtenemos en 2-complemento el número
negativo -3, el cual podemos sumar directamente (¡en suma binaria, no suma Boleana!) al número positivo +2 para obtener "
11111111",
que es equivalente en 2-complemento del número -1 (en 8 bits).
El resultado de la operación aritmética está dado, como vemos, en 2-complemento, y es un número negativo. Obsérvese cómo en esta ocasión sí obtuvimos los resultados aritméticos correctos.
Para que el procedimiento quede claro, hagamos una segunda operación usando 5 bits, sumando los números +13 y -9. Al número 13, por ser positivo, lo dejamos tal cual; su equivalente binario es
01101. El número 9, por ser negativo, debe ser convertido a su representación como
2-complemento. El equivalente binario de 9 es
01001; su
1-complemento es
10110, y su 2-complemento es
10111. Si sumamos
01101 y 1
0110, obtenemos
00100, o sea +4, que es el resultado correcto de acuerdo a los signos originales, con la respuesta también teniendo el signo correcto.
Hay pues tres tipos de operaciones aritméticas involucrando signos: (1) la adición de dos números positivos, (2) la adición de un número positivo y uno negativo, o lo que es lo mismo, una operación de resta, y (3) la adición de tres números negativos; y el método del
2-complemento trabaja en los tres casos como lo resumen los siguientes tres ejemplos:
La ventaja de utilizar la representación del
2-complemento es que uno no se tiene que preocupar por el bit del signo al llevar a cabo operaciones aritméticas de suma y resta;
el resultado final siempre será correcto independientemente de los signos de los números. El no tener que estar probando explícitamente el signo de los números binarios al llevar a cabo operaciones aritméticas puede resultar en una mejora substancial de velocidad cuando este tipo de operaciones son llevadas a cabo por circuitos lógicos.
Solo resta hacer una última advertencia con respecto al uso del símbolo "=" (igual) en el álgebra Boleana. Dicho símbolo nos dice que dos expresiones conectadas por él, por ejemplo:
son
equivalentes en álgebra Boleana (ambas producen la misma Tabla de Verdad)
pero no iguales en el concepto de uso común en el álgebra clásica.
Esto quiere decir que las siguientes operaciones válidas en el álgebra
clásica:
son
incorrectas en el álgebra Boleana. En efecto, dada una expresión en álgebra Boleana, podemos simplificarla usando los teoremas vistos anteriormente, relacionando cada nueva expresión con la anterior usando el símbolo de
equivalencia "=". Sin embargo, las simplificaciones como la arriba mostrada carecen de todo sentido en el álgebra Boleana.