(1) F(a,b,c) = Σm(0,2,7)
(2) F(A,B,C,D) = Σm(0,1,3,4,5,7,12,13,15)
(3) F(A,B,C,D) = Σm(15,11,7,14,10,12,6,4)
(4) Z = Σm(0,1,2,4,6)
En el primer caso que involucra a tres variables, la expresión Boleana explícita será:
F(a,b,c) = Σm(000,010,111)
F(a,b,c) = a∙b∙c + abc + abc
En el segundo caso, la expresión Boleana explícita será:
F(A,B,C,D) = Σm(0000,0001,0011,0100,0101,0111,1100,1101,1111)
F(A,B,C,D) = A∙B∙C∙D + A∙B∙CD + A∙BCD + ABC∙D + ABCD
+ ABCD + ABC∙D + ABCD + ABCD
En el tercer caso, la expresión Boleana explícita será:
F(A,B,C,D) = Σm(1111,0111,1110,1010,1100,0110,0100)
F(A,B,C,D) = ABCD + ABCD + ABCD + ABCD + ABC∙D + ABCDD + ABC∙D
Y en el cuarto caso que podemos suponer que involucra a tres variables puesto que el decimal más grande de todos no excede de 7 (111), designando a dichas variables como p, q y r la expresión Boleana explícita será:
Z = Σm(000,001,010,100,110)
Z = p∙q∙r+ p∙q + pqr + pq∙r + pqr
Z = p∙q∙r+ p∙q + pqr + pq∙r + pqr
PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.
Z = A∙B∙C + A∙B∙C + AB∙C + ABC
Usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con la cual:
Z = Σ(000,001,100,101)
Z = Σm(0,1,4,5)
Z = Σm(0,1,4,5)
Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:
En la segunda lista podemos ver que la expresión original ha sido reducida a:
Z = A∙B + B∙C + BC + AB
Y en la tercera lista vemos que la expresión final simplificada es Z=B.
En este caso, dada la simplicidad de la minimización, no fue necesario trazar ninguna retícula.
PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.
Z = A∙B∙CD + A∙BCD + ABCD + ABCD' + ABCD + ABCD' + A∙BCD
Por comodidad, usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con lo cual:
Z = Σm(0000,0010,0100,0101,1000,1001,1100)
Z = Σm(0,2,4,5,8,9,12)
Z = Σm(0,2,4,5,8,9,12)
Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:
De la simplificación sucesiva podemos ver que los implicantes primarios de la expresión Boleana original son A∙B∙D, ABC, AB∙C y C∙D.
Finalmente, y aunque no es indispensable en este problema, construímos una retícula con la finalidad de confirmar que ninguno de los implicantes primarios obtenidos es redundante:
Podemos ver que la solución final de la minimización es entonces:
Z = A∙B∙D + ABC + AB∙C + C∙D
PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.
Z = A∙B∙C∙D + A∙B∙CD + A∙BCD + A∙BCD + ABCD + ABCD
+ AB∙C∙D + ABCD + ABC∙D + ABCD + ABCD
Nuevamente, por comodidad usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con lo cual:
Z = Σm(0000,0001,0010,0011,0101,0111,1000,1010,1100,1101,1111)
Z = Σm(0,1,2,3,5,7,8,10,12,13,15)
Z = Σm(0,1,2,3,5,7,8,10,12,13,15)
Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:
De la simplificación sucesiva podemos ver que los implicantes primarios de la expresión Boleana original son A∙B, B∙D, AD, BD, AC∙D y ABC. Finalmente, construímos una retícula con la finalidad de remover a los implicantes primarios redundantes:
Podemos ver que la solución final de la minimización, con los implicantes primarios redundantes ya removidos, es entonces:
Z = B∙D + BD + A∙B + AC∙D
PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.
Z = A∙B∙C∙D + A∙B∙CD + A∙BCD + A∙BCD + ABC∙D + ABCD
+ ABCD + AB∙CD' + AB∙CD + ABCD + ABCD
+ ABCD + AB∙CD' + AB∙CD + ABCD + ABCD
Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de la primera lista que aparece en el extremo izquierdo a la segunda lista en donde puede apreciarse que los términos de cuatro variables han sido reducidos a términos de tres variables, pasando finalmente a la tercera lista en el extremo derecho en la cual los términos de tres variables han sido reducidos a términos de dos variables:
Finalmente, construímos la retícula en la cual "graficamos" los implicantes primarios obtenidos en su relación con los minterms de la expresión original:
De la reticula podemos ver que la expresión final simplificada es:
Z = B∙C + A∙D + CD
El método de Quine-McCluskey es superior al mapa de Karnaugh en el sentido de que el primero se presta a ser programado para ser resuelto de manera automática por una computadora. Repasando los problemas anteriores, cualquiera que tenga conocimientos previos en programación en algún lenguaje como BASIC ó C++ podrá ir formando ya en su mente un algoritmo ("receta de cocina" generalizada especificando una serie de pasos para la resolución de un problema computacional) para llevar a cabo la minimización de un circuito lógico en forma automatizada mediante el método Quine-McCluskey, el cual siempre garantiza la obtención de la configuración mínima. Sin embargo, el principal problema con el método de Quine-McCluskey, visible ya para alguien con conocimientos de programación que quiera elaborar su programa para generalizar el método hacia cualquier número de variables, es que tiene que llevar a cabo una búsqueda exhaustiva agotando una por una todas las posibilidades, lo cual en la materia clásica de Estructuras de Datos equivale a tener que recorrer todos los nodos de un "árbol" que se va formando al irse acumulando los resultados parciales obtenidos en la búsqueda de la solución óptima. Esto, desde luego, pone al método de Quine-McCluskey dentro de una categoría de problemas matemáticos conocidos como NP-"duros", lo cual en términos llanos significa que el algoritmo de Quine-McCluskey va creciendo exponencialmente de acuerdo a la cantidad de variables de entrada aumentando enormemente la cantidad de tiempo computacional requerido a medida que aumenta la cantidad de entradas a un circuito lógico, lo cual eventualmente limita el rango de aplicación del método.
PROBLEMA: Así como hay una notación compacta para representar una expresión Boleana puesta en función de sus minterms como una suma de productos, también hay una notación compacta para representar una expresión Boleana puesta en función de sus maxterms como un producto de sumas. Bajo esta notación, la siguiente expresión Boleana escrita empleando maxterms, como un producto de sumas:
Salida = (A + B + C)(A + B + C)
puede ser convertida a notación compacta recordando la manera en la cual se definen los maxterms a partir de una Tabla de Verdad (recuérdese que en un maxterm la suma Boleana de las variables debe ser siempre cero, debiéndose complementar aquellas variables que sean "1" para que así haya únicamente "ceros" en la formación del maxterm). Así, la expresión dada arriba queda representada en forma compacta de la siguiente manera:
Salida = ΠM(000,001)
o bien, usando la más familiar notación decimal:
Salida = ΠM(0,1)
Revirtiendo los pasos, podemos reconstruír la expresión original. Obsérvese que se ha utilizado la letra griega Pi mayúscula (Π) para indicar que se trata de un producto de sumas. El par "ΠM" se lee como "el producto de maxterms".
Definido lo anterior, representar en forma compacta las siguientes expresiones:
(1) F(A,B,C) = (A + B + C) ∙ (A + B + C)
(2) F(A,B,C,D) = (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D)
(2) Z = (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D)
__________∙ (A+B+C+D) ∙ (A+B+C+D)
Para la primera expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con la combinación de "unos" y "ceros" que lo producirían en una Tabla de Verdad:
F(A,B,C) = ΠM(101,110)
F(A,B,C) = ΠM(5,6)
F(A,B,C) = ΠM(5,6)
Para la segunda expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con lo que lo produciría en una Tabla de Verdad:
F(A,B,C,D) = ΠM(0101,1000,0011,1001)
F(A,B,C,D) = ΠM(5,8,3,9)
Reacomodando:
F(A,B,C,D) = ΠM(3,5,8,9)
Para la tercera expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con lo que lo produciría en una Tabla de Verdad:
Z = ΠM(0010,0110,1110,1010,1000,1001,1011)
Z = ΠM(2,6,14,10,8,9,11)
Z = ΠM(2,6,14,10,8,9,11)
Reacomodando:
Z = ΠM(2,6,8,9,10,11,14)
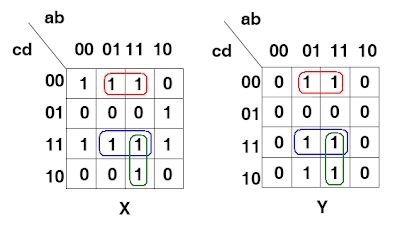
PROBLEMA: Encontrar, para un circuito de dos salidas con cuatro variables de entrada, cuyos mapas de Karnaugh sean los siguientes:
los agrupamientos comunes que podrían ser utilizados para formar sub-circuitos comunes reduciendo con ello la cantidad de componentes y alambrado requerido.
Con ambos mapas de Karnaugh puestos lado a lado, podemos captar de inmediato las siguientes tres regiones comunes (una encerrada en una línea roja, la otra en una línea verde, y la otra en una línea azul) que podrían ser utilizadas para formar sub-circuitos:
Obsérvese que no estamos utilizando aquí el mapa de Karnaugh en su sentido "clásico" para minimizar una función Boleana dentro del mapa, sino para detectar las regiones comunes en mapas diferentes. Sin embargo, una vez detectadas las regiones comunes a mapas diferentes, podemos tratar de minimizar dichas regiones comunes dentro de cada mapa (la simplificación en todo caso será la misma para regiones iguales). Esta técnica se puede extender a circuitos lógicos con tres, cuatro, cinco o más salidas. El inconveniente de ir extendiendo este método a una cantidad mayor de variables de salida es que con muchos mapas de Karnaugh puede ir resultando más difícil captar las regiones comunes.