PROBLEMAS RESUELTOS SOBRE CONTADORES , FLIP-FLOP (J-K): PARTE 1ª

PROBLEMA: Dados los siguientes diagramas de tiempo para el flip-flop J-K, obténganse los diagramas de tiempo a la salida del mismo en las terminales Q y Q a partir de los diagramas de tiempo proporcionados. Supóngase que el flip-flop J-K está inicialmente en el estado Q=0. Supóngase también que los cambios son motivados por las transiciones de "1" a "0" en la terminal C y que en el estado J=1 y K=1 la terminal C no ejerce ninguna acción.

La salida en la terminal Q basada en las características del flip-flop J-K suponiendo que inicialmente Q=0 es como se muestra a continuación:

La explicación del diagrama de tiempos de la salida Q es la siguiente:

Suponiendo que el flip-flop J-K está inicialmente en el estado Q=0, la transición de "0" a "1" en la terminal C no produce efecto alguno, pero la caída subsecuente de "1" a "0" hace que el flip-flop J-K cambie de estado, pasando de Q=0 a Q=1. La siguiente transición negativa de "1" a "0" en la terminal C hace que la salida Q vuelva a cambiar de estado, pasando de Q=1 a Q=0. Tras esto, aparecen unos "pulsos" en las terminales J y K, pero estos no tienen efecto alguno al permanecer la terminal C en un nivel estático. Tras ascender nuevamente la terminal C de "0" a "1", hay un cambio en el valor de entrada en la terminal J, que es puesta a J=1. Esto prepara al flip-flop para que cuando haya una transición negativa de "1" a "0" en la terminal C el flip-flop J-K pase al estado Q=1 al tener J=1 y K=0 en sus terminales de entrada, que es precisamente lo que ocurre al final del tercer "pulso" en la terminal C. Tras esto, después de que la entrada en la terminal J cae de "1" a "0" sin producir cambio alguno puesto que los cambios los produce únicamente la terminal C, la terminal C sube de "0" a "1" sin producir todavía cambio alguno en la salida, y permanece en "1" mientras el valor en la terminal K sube de "0" a "1". Esto prepara al flip-flop para que cuando haya una transición negativa de "1" a "0" en la terminal C el flip-flop J-K pase al estado Q=0 al tener J=0 y K=1 en sus terminales de entrada, que es precisamente lo que ocurre al final del cuarto "pulso" en la terminal C. Tras esto, la entrada J es elevada de "0" a "1", con lo cual ambas entradas J y K tienen el valor de "1", lo cual tiene como consecuencia directa que cuando ocurran los siguientes dos "pulsos" en la señal de "reloj" C el flip-flop J-K no cambie de estado.

Puesto que la salida en la terminal Q es simplemente el complemento (inverso lógico) de la salida en la terminal Q, el aspecto del diagrama de tiempos mostrado por esta terminal será el siguiente:

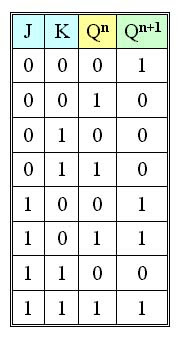
PROBLEMA: Demostrar que la salida de un flip-flop J-K, después de que ha ocurrido una transición, está dada por:

Qⁿ⁺¹ = JQⁿ + K·Qⁿ

en donde Qⁿ es la salida del flip-flop J-K antes de llevarse a cabo la transición.

Tomando en cuenta las propiedades del flip-flop J-K, se puede desarrollar la siguiente Tabla de Verdad:

De la Tabla de Verdad se puede obtener ahora Qⁿ⁺¹ en función de J, K y Qⁿ por medio de minterms:

Qⁿ⁺¹ = J·K·Qⁿ + J·K·Qⁿ + J·K·Qⁿ + JKQⁿ

Qⁿ⁺¹ = (J + J)·K·Qⁿ + (K + K)JQⁿ

Qⁿ⁺¹ = JQⁿ + K·Qⁿ

PROBLEMA: Diseñar un flip-flop J-K usando funciones lógicas básicas, utilizando para ello bloques NOR.

Para facilitar la comprensión del diseño, se reproducen primero el diagrama esquemático y la Tabla de Verdad del flip-flop R-S hecho con bloques NOR:

Es necesario diseñar primero una configuración en la cual la información a la entrada sea transferida a la salida únicamente cuando la terminal de "reloj" C vaya del estado "1" al estado "0", justo cuando ocurre la transición. Esto presupone necesariamente dos pasos, a saber:

(A) Cuando la terminal C va de "0" a "1".- La configuración es "preparada" para el cambio que habrá de ocurrir. Se almacena dentro de la configuración interna del elemento la información que está puesta a la entrada del mismo.

(B) Cuando la terminal C va de "1" a "0".- La salida de la configuración adquiere el estado a su entrada que fue almacenado por la misma durante la transición de "0" a "1". Esto sugiere el uso de dos flip-flops R-S para construír la configuración.

Para poder implementar lo anterior, se requiere un circuito con dos flip-flops R-S en una configuración maestro-esclavo (master-slave) como se muestra a continuación:

El tipo de compuerta usado debe permitir el flujo de información al ser activada con un "1" y detener todo flujo de información al ser desactivada con un "0". Al ser desactivada con un "0", su salida en sus dos terminales debe ser "0" para que el flip-flop R-S que le sigue retenga al información que se deseaba almacenar (o sea, viendo la Tabla de Verdad del flip-flop R-S hecho con bloques NOR, se requiere que R=0 y S=0 para que el flip-flop retena su estado anterior). Este tipo de compuerta ya lo hemos visto previamente. Se puede construír fácilmente usando funciones AND como se muestra a continuación:

Al ir la terminal C de "0" a "1", la compuerta de entrada permite que se almacene en el flip-flop maestro la información a la entrada de la configuración, a la vez que la compuerta de transferencia entre los dos flip-flops impide que esta información altere la información que está puesta a la salida de la configuración, porque se requiere que la salida permanezca inalterada en la transición positiva de la señal de "reloj".

Al ir la terminal C de "1" a "0", la compuerta de transferencia permite que el flip-flop maestro "imponga" su estado en el flip-flop esclavo, a la vez que la compuerta de entrada detiene todo nuevo flujo de información a la entrada de la configuración, conservando así el flip-flop maestro su estado que está siendo transmitido al flip-flop esclavo.

En el siguiente gráfico animado (ampliar imagen para poder ver la animación en acción) se muestra una configuración "maestro-esclavo" de flip-flops hechos con bloques NAND:

En el extremo superior izquierdo tenemos la simulación de un osciloscopio actuando como analizador lógico que nos permite ver el pulso que está siendo aplicado en la terminal de "reloj" C a la entrada del circuito. Obsérvense las dos acciones que ocurren cuando (a) el pulso de entrada va de "0" a "1", y (b) cuando va de "1" a "0".

Falta ahora relacionar las entradas S₀ y R₀ del circuito con las terminales J y K externas al circuito que le vamos a agregar y que eventualmente identificaremos como las terminales J y K, tomando en cuenta el estado en el cual se encuentra la salida Q del segundo flip-flop (el flip-flop esclavo) que vendría siendo la salida de todo el circuito.

Cuando J=1 y K=0, si Q=0 entonces después de una transición el circuito quedará en el estado Q=1. Para que esto ocurra en nuestra configuración se requiere que S₀=1 y R₀=0. Representando esto en una Tabla de Verdad:

Cuando J=1 y K=0, si Q=1 entonces el flip-flop J-K conservará su estado sin que lo afecten las transiciones en la terminal C. En nuestra configuración esto equivale a tener S₀=0 y R₀=0 para que retenga su estado y sea inmune a las transiciones en la terminal C. Por lo tanto:

Usando razonamientos como los anteriores, encontramos también que:

Cuando J=1 y K=1, el flip-flop J-K retiene su estado anterior (ya sea Q=1 ó Q=0) sin que lo afecten las transiciones en la terminal C. Para lograr el mismo efecto, nuestra configuración requiere S₀=0 y R₀=0. Por lo tanto:

Cuando J=0 y K=0, el flip-flop J-K cambia de estado después de cada transición. Si J=0, K=0 y Q=0, el flip-flop J-K cambiará al estado Q=1 después de una transición, efecto que obtenemos en nuestro circuito con S₀=1 y R₀=0. Por lo tanto:

Asimismo, cuando J=0, K=0 y Q=1, el flip-flop J-K cambiará al estado Q=0 después de una transición, lo cual se logra en nuestro circuito con con S₀=0 y R₀=1. Por lo tanto:

Juntando toda la información anterior en una sola Tabla de Verdad:

Podemos ahora obtener los valores Boleanos que deben tener S₀ y R₀ en función de los valores que tengan J y K para que nuestra configuración se pueda comportar como un flip-flop J-K. Usando minterms:

S₀ = J·K·Q + J·K·Q

S₀ = (J + J)K·Q

S₀ = K·Q

S₀ = K + Q

y

R₀ = J·K·Q + JKQ

R₀ = JQ(K + K)

R₀ = JQ

En esta última línea podemos aplicar "a la inversa" una de las leyes de DeMorgan de la siguiente manera:

para obtener así una expresión final para R₀ que se pueda construír mediante un bloque NOR.

Con estas dos relaciones para S₀ y R₀ implementables con bloques NOR (éste fue a fin de cuentas el objetivo verdadero detrás de las manipulaciones Boleanas mostradas), las cuales llevan a cabo primero la suma Boleana de las entradas y tras esto efectúan el complemento de la suma, podemos ver que el diseño del circuito toma ahora el siguiente aspecto:

PROBLEMA: Con la ayuda de un analizador lógico, un técnico obtiene en la carátula del analizador los siguientes diagramas de tiempo para un flip-flop J-K:

¿Qué tipo de flip-flop J-K es el que describen estos diagramas de tiempo? Explicar en detalle lo que está sucediendo desde el principio hasta el final de los diagramas de tiempo.

Comparando los pulsos de entrada en la terminal de reloj C (clock) con lo que ocurre a la salida Q del flip-flop, es obvio que las transiciones ocurren para este flip-flop cuando la señal de reloj va de "0" a "1" en vez de ocurrir cuando va de "1" a "0". Este flip-flop J-K es por lo tanto uno activado por las transiciones positivas (de "0" a "1") en la terminal de "reloj".

Al principio, la terminal J sube de "0" a "1". Pero como no es esta terminal la que produce las transiciones, no ocurre nada. Tras esto, la señal de "reloj" sube de "0" a "1", y por estar las entradas del flip-flop J-K puestas a J=1 y K=o cuando esto ocurre, el flip-flop que estaba en el estado Q=0 pasa al estado Q=1, mientras que su salida complementaria que estaba en el estado Q=1 pasa al estado Q=0. Una vez que esto ha ocurrido, la entrada J es bajada de "1" a "0" y tras esto la entrada K es subida de "0" a "1", de modo tal que cuando la señal de "reloj" sube de "0" a "1" estando puestas las entradas a J=0 y K=1 en el siguiente ascenso positivo del pulso posterior del "reloj" el estado Q=1 pasa a ser el estado Q=0, mientras que la salida complementaria que estaba en el estado Q=0 pasa al estado Q=1. Posteriormente la señal en la entrada K cae de "1" a "0" y vuelve a subir de "0" a "1", lo cual por sí solo no tiene efecto alguno en el comportamiento del flip-flop, y al ocurrir la tercera transición positiva del pulso de reloj las entradas están a los mismos valores J=0 y K=1 que tenían en la transición anterior, de manera que no se manifiesta cambio alguno. Entre el tercer y el cuarto pulso de reloj hay transiciones en las terminales J y K que no producen cambio alguno, como era de esperarse. En la cuarta transición positiva de la señal de reloj las terminales J y K están ambas al mismo valor de "1", y se produce una transición de Q=1 a Q=0, repitiéndose los cambios que hacen que el flip-flip J-K transite entre estados opuestos con cada transición positiva de la señal de reloj. Esto nos confirma que el flip-flop J-K está construído con bloques NAND.


PROBLEMA: Ilustrar una manera en la cual se pueda poner de modo "forzado" al flip-flop J-K ya sea en el estado Q=0 o en el estado Q=1 sin necesidad de tener que utilizar la terminal C.
Tomando como base el diseño previo de un flip-flop J-K construído con bloques NOR, esto se puede lograr usando flip-flops de tres entradas en lugar de dos en el flip-flop esclavo de la configuración. Dicho elemento tomará el siguiente aspecto:

Estudiando la configuración y tomando en cuenta las propiedades del flip-flop J-K hecho con bloques NOR, encontramos que al activar la terminal R_d de acción "directa" hacia la salida Q con un "1", el flip-flop J-K es forzado a entrar en la condición Q=0. Asimismo, al activar la terminal S_d con un "1" el flip-flop J-K es forzado a entrar en la condición Q=1. Se puede observar que ambas terminales R_d y S_d no deben ser activadas al mismo tiempo, ya que se colocaría al flip-flop esclavo interno (y por lo tanto al flip-flop J-K en un estado no-definido. También podemos observar que mientras una de las terminales permanezca activada, el flip-flop J-K no responderá a los valores que tomen las entradas J, K y C.

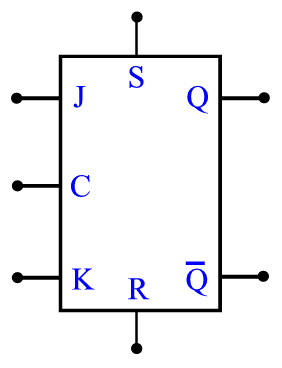
Una forma de representar un flip-flop J-K con terminales de "limpieza" R y "preajuste" S directas es como sigue:

Nótese que la cercanía de la terminal S con la salida Q sugiere que al ser activada S el "1" con el cual es activada pasa a la salida más cercana que es en este caso Q. De la misma manera, al ser activada R, el "1" con el cual es activada pasa a Q.

En la literatura técnica es frecuente llamar a las terminales R y S como "clear" y "preclear". Desafortunadamente, al abreviar el símbolo de la terminal de "limpieza" clear con la letra C (de clear) se puede confundir con el símbolo para la terminal de reloj C que para evitar confusiones a veces es redesignada como CLK.

Los circuitos integrados comerciales flip-flops J-K puestos a la venta generalmente tienen incluídas estas terminales de "limpieza", y como ejemplo de ello se puede citar el circuito integrado 4027 fabricado con tecnología CMOS:

el cual incluye dos flip-flops J-K (simbolizados en el diagrama como F/F). En el flip-flop 1, el equivalente de nuestra terminal S que forza al flip-flop a entrar en el estado Q=1 está puesto en la terminal 9 del circuito integrado (SET 1), mientras que el equivalente de nuestra terminal R que "limpia" al flip-flop poniéndolo en el estado Q=0 está puesto en la terminal 12 del circuito integrado (RESET 1).

El uso de terminales de "limpieza" en cada circuito de memoria es sumamente útil cuando se enciende un sistema digital que había estado apagado por algún tiempo, ya que durante el proceso de encendido cada uno de los elementos de memoria puede entrar en un estado de "1" ó en un estado de "0" de manera completamente aleatoria, lo cual podría ser reinterpretado erróneamente por el sistema al empezar a funcionar. La "limpieza" de todos los registros de memoria garantiza de que no habrá nada en los registros que pueda ser malinterpretado durante el procedimiento de arranque. Este proceso de "limpieza" es precisamente lo que se lleva a cabo cada vez que se enciende una computadora de escritorio o que se oprime el botón de RESET (en las que lo tienen) para volver a comenzar de nuevo desde cero, literalmente, en todos los registros de memoria.


PROBLEMA: La siguiente configuración de flip-flops J-K recibe un tren simétrico de pulsos en la terminal de entrada C del primer flip-flop J-K. Suponiendo que los flip-flops están inicialmente en el estado Q₁Q₂Q₃=000, constrúyase un diagrama de tiempos y a partir del mismo constrúyase una tabla de secuencias en el orden Q₃Q₂Q₁.

¿Qué conclusiones se puede sacar de los resultados obtenidos?

Por tener "ceros" en sus dos entradas J y K, con un tren simétrico de pulsos en la entrada C el primer flip-flop cambiará de estado de Q₁=0 a Q₁=1 y otra vez de Q₁=1 a Q₁=0 cada vez que la entrada caiga de "1" a "0". Puesto que la salida de Q₁ es a su vez la entrada en la terminal C del segundo flip-flop, el cual también tiene en sus dos entradas J=0 y K=0, este cambiará de estado de Q₂=0 a Q₂=1 y otra vez de Q₂=1 a Q₂=0 cada vez que la salida de Q₁ caiga de "1" a "0". Y una situación similar aplica al tercer flip-flop. Así pues, el diagrama de tiempos para un tren simétrico de pulsos en la terminal de entrada C empezando con el estado Q₁Q₂Q₃=000 hasta regresar al mismo estado será como se muestra a continuación:

Tomando en cuenta este diagrama de tiempos, la tabla de secuencias correspondiente es la que se muestra a continuación:

Podemos observar de la tabla de secuencias que la configuración presentada es básicamente un contador binario. Tenemos así un circuito lógico que va contando hacia arriba en el sistema de la numeración binaria, la cual fue introducida en el primer capítulo de este libro. Es de esperarse, por lo tanto, que esta configuración tenga aplicaciones importantes en muchos sistemas digitales (y así es, en efecto). Nótese que con tres flip-flops J-K se puede contar en sistema binario en una palabra de tres bits. Por regla general, se puede contar en sistema binario en una palabra de n bits con n flip-flops J-K.


PROBLEMA: La siguiente configuración de flip-flops J-K recibe un tren simétrico de pulsos en la terminal de entrada C del primer flip-flop J-K. Suponiendo que los flip-flops están inicialmente en el estado Q₁Q₂Q₃=111, constrúyase un diagrama de tiempos y a partir del mismo constrúyase una tabla de secuencias en el orden Q₃Q₂Q₁.

¿Qué conclusiones se pueden sacar de los resultados obtenidos?

Este problema es muy parecido al problema anterior. Por tener "ceros" en sus dos entradas J y K, con un tren simétrico de pulsos en la entrada C el primer flip-flop cambiará de estado de Q₁=0 a Q₁=1 y otra vez de Q₁=1 a Q₁=0 cada vez que la entrada caiga de "1" a "0". Sin embargo, es la salida complementaria Q₁' del primer flip-flop la que está alimentando la entrada C del segundo flip-flop. Por esta razón, el segundo flip-flop cambiará de estado de Q₂=0 a Q₂=1 y otra vez de Q₂=1 a Q₂=0 cada vez que la salida de Q₁ caiga de "1" a "0". Y una situación similar aplica al tercer flip-flop. Así pues, el diagrama de tiempos para un tren simétrico de pulsos en la terminal de entrada C empezando con el estado Q₁Q₂Q₃=111 hasta regresar al mismo estado será como se muestra a continuación:

Tomando en cuenta este diagrama de tiempos, la tabla de secuencias correspondiente es la que se muestra a continuación:

PROBLEMA: El Registro de Transferencia. Analizar la siguiente configuración suponiendo que ésta recibe un tren simétrico de pulsos en la terminal de entrada. Supóngase que las entradas J y K del primer flip-flop mantienen un valor constante de "0" y "1" respectivamente. Supóngase también que el circuito está inicialmente en el estado Q₁Q₂Q₃Q₄=1011. Constrúyase una tabla de secuencias para la sucesión de eventos.

Siendo la condición inicial Q₁Q₂Q₃Q₄=1011, se tiene al comenzar la siguiente situación:

Antes que nada, notamos que las entradas en las terminales J y K de cada flip-flop son complementarias entre sí. En esta circunstancia, Q tomará el valor de J después de una transición de "1" a "0" en cada flip-flop. En la primera transición, el flip-flop 4 toma el valor Q₃ a la salida del flip-flop 3, produciendo Q₄=1, el flip-flop 3 toma el valor del flip-flop 2 produciendo Q₃=0, el flip-flop 2 toma el valor del flip-flop 1 produciendo Q₂=1 y el flip-flop 1 toma el valor de "0" que está puesto en su entrada J produciendo Q₁=0. Esta cadena de eventos es posible debido a que hay un retardo de tiempo dentro de cada flip-flop que después de la transición "retarda" la información el tiempo suficiente para que la información a su salida pueda ser leída por el flip-flop que le sigue.

Pictóricamente, esto se puede representar de la siguiente manera imaginando el recorrido de la información a través de cada flip-flop (inmediatamente después del comienzo de una transición) como área sombreada de color amarillo:

Podemos ver en forma rudimentaria con el mecanismo arriba mostrado cómo es posible que un flip-flop "lea" información de otro flip-flop que le precede reteniendo al mismo tiempo la información a su salida el tiempo suficiente para que el siguiente flip-flop la pueda leer. Visto esto, podemos continuar con el análisis para observar lo que ocurre después de cada transición.

Primera transición:

La condición es Q₁Q₂Q₃Q₄=0101.

Segunda transición:

La condición es Q₁Q₂Q₃Q₄=0010.

Tercera transición:

La condición es Q₁Q₂Q₃Q₄=0001.

Cuarta transición:

La condición es Q₁Q₂Q₃Q₄=0000.

La quinta transición y las transiciones subsecuentes no lograrán sacar al circuito del estado Q₁Q₂Q₃Q₄=0000, de manera que en este punto detenemos el análisis.

La tabla de secuencias para cada transición sucesiva empezando con la condición Q₁Q₂Q₃Q₄=1011 será, basada en los resultados obtenidos, como se muestra a continuación:

Podemos ver que después de cada transición, la palabra almacenada originalmente es desplazada un bit hacia la derecha, siendo enviada al mundo exterior por el último flip-flop (el flip-flop 4). Circuitos de este tipo reciben el nombre de registro de transferencia (ó registro de desplazamiento, ó registro de corrimiento y tienen aplicaciones importantes en los circuitos lógicos. En este caso, el registro de transferencia (shift register) fué usado para leer una palabra almacenada en forma serial (esto es, bit por bit). El registro de transferencia también puede ser usado para escribir en el mismo una palabra introduciéndola bit por bit en el primer flip-flop (el flip-flop 1) para su uso subsecuente.


PROBLEMA: Ilustrar la manera en la cual se puede evitar perder la información contenida en un registro de transferencia al ir sacando la información del registro en forma serial. Construír una tabla de secuencias para mostrar la acción del circuito, usando la palabra 10110 como base.

La forma en la cual se puede evitar perder la información que va saliendo fuera es conectando la salida del circuito (el Registro de Transferencia) que provee la información a la entrada del mismo. Bajo este esquema, la terminal Q del último flip-flop J-K es conectada a la terminal J del primer flip-flop, y la terminal Q del último flip-flop es conectada a la terminal K del primer flip-flop. La idea esencial es la siguiente:

De esta manera, después de la primera transición, el último bit que estaba a la salida del registro es almacenado a la entrada en el primer flip-flop, cuyo lugar estaba vacante por haberse recorrido la palabra de n bits un bit a la derecha. En las transiciones subsecuentes, los bits a la salida van "rellenando" los lugares vacantes que va dejando la palabra al irse recorriendo a la derecha bit por bit. Después de n transiciones, la palabra habrá sido "recuperada" por el Registro y, además, ha sido proporcionada como información bit por bit en forma serial al mundo exterior.

Este tipo de registros se conoce comunmente como registro recirculante.

Un registro recirculante con capacidad de almacenamiento de 3 bits se muestra a continuación:

Una tabla de secuencias para la acción de este tipo de circuito empezando con la palabra 10110 será como la que se muestra a continuación:

PROBLEMA: Explicar en detalle el diagrama de tiempos mostrado para el siguiente registro de desplazamiento. (La imagen tiene acción animada para ayudar a captar mejor lo que está sucediendo, siendo necesario llevar a cabo el procedimiento de ampliar imagen para poder ver la animación.)

La explicación se dará tomando como punto de referencia los tiempos numerados del 1 al 11 puestos encima del diagrama de tiempos.

Al comienzo del tiempo 1, la única señal de entrada a cada uno de los flip-flops J-K mostrados es un "1" puesto mediante la terminal "Reset" del circuito a través del alambre rojo. Puesto que la entrada de este "1" en cada flip-flop es complementada como R, entonces lo que viene entrando a fin de cuentas es un "0" como señal de "Reset", el cual no tiene efecto alguno en ninguno de los cuatro flip-flops.

Al comienzo del tiempo 2, se aplica un "1" en la terminal "Set" del circuito y se aplica también un "1" en la terminal S₁ a la entrada del primer NAND, cuya salida va conectada al primer flip-flop (en el extremo izquierdo del circuito). Los dos "1" puestos a la entrada del NAND son convertidos a un "0" a la salida del mismo, el cual al ser complementado como S en el primer flip-flop le viene poniendo un "1" en su terminal de "Set". Esto forza la salida Q₁ del primer flip-flop a tomar el valor de "1". Los tres flip-flops restantes no experimentan cambio alguno por tener cada una de las terminales S₂, S₁ y S₄ un "0", lo cual produce un "1" a la salida de cada uno de los NANDs restantes que se convierte en un "0" en las entradas complementadas S de los flip-flops restantes.

Al terminar el tiempo 2 y comenzar el tiempo 3, las señales de "1" son removidas de las terminales "Set" y S₁ del circuito, a la vez que se aplica el inicio de un pulso de reloj en la terminal "Shift", el cual aún no tendrá efecto alguno puesto que los cambios ocurren en las transiciones de la señal de reloj de "1" a "0" y no cuando va de "0" a "1".

Al terminar el tiempo 3 y comenzar el tiempo 4, bajo la acción de la caída de "1" a "0" del pulso de reloj aplicado en la terminal "Shift" la salida Q₁ del primer flip-flop pasa a la entrada J del siguiente flip-flop a su derecha poniéndolo en el estado Q₂=1, mientras que el primer flip-flop entra en el estado Q₁=0 al estar siendo alimentado en su terminal J con el "0" que está poniendo el último flip-flop en su salida Q₄. Los dos flip-flops intermedios permanecen con salidas de "0".

Al terminar el tiempo 4 y empezar el tiempo 5 se aplica nuevamente en la terminal "Shift" el inicio de otro pulso de reloj, aunque de nueva cuenta no ocurre nada puesto que se supone que para todos estos flip-flops los cambios ocurren en las transiciones de la señal de reloj de "1" a "0".

Al terminar el tiempo 5 y comenzar el tiempo 6, con la caída del pulso de reloj de "1" a "0" la salida del segundo flip-flop pasa al siguiente flip-flop a su derecha poniéndolo en el estado Q₃=1, mientras que los flip-flops precedentes entran en los estados Q₁=0 y Q₂=0. El flip-flip con salida Q₄ también permanece en el estado "0".

Al terminar el tiempo 6 y comenzar el tiempo 7, se aplica en la terminal "Shift" el inicio del siguiente pulso de reloj, pero no ocurre nada puesto que los cambios en los flip-flops ocurren en las transiciones de la señal de reloj de "1" a "0".

Al terminar el tiempo 7 y comenzar el tiempo 8, con la caída del pulso de reloj de "1" a "0" la salida de Q₃=1 del tercer flip-flop pasa al cuarto flip-flop, a su derecha, poniéndolo en el estado Q₄=1, mientras que todos los flip-flops precedentes entran en los estados Q₁=0, Q₂=0 y Q₃=0.

Al terminar el tiempo 8 y comenzar el tiempo 9, la aplicación simultánea de un "1" en la terminal "Set" del circuito y de un "1" en las terminales S₁, S₂, S₃ y S₄ tiene el efecto de forzar a todos los flip-flops J-K a entrar en los estados Q₁=1, Q₂=1, Q₃=1 y Q₄=1 por las razones señaladas al principio.

Al terminar el tiempo 9 y comenzar el tiempo 10, aunque los "1" puestos en las terminales de "Set", S₁, S₂, S₃ y S₄ son removidos, los flip-flops permanecerán en sus estados con salidas de "0", puesto que este es precisamente el objetivo de una señal de "Set" o "Ajuste" a "1". Y permanecerán en dichos estados hasta el inicio del tiempo 11.

Por último, al comenzar el tiempo 11, la terminal "Reset" de todo el circuito cae de "1" a "0". Puesto que este "0" entra a cada flip-flop J-K complementado como R, entonces lo que viene entrando a fin de cuentas es un "1" como señal de "Reset", lo cual tiene el efecto de forzar a todos los flip-flops J-K a entrar en los estados Q₁=0, Q₂=0, Q₃=0 y Q₄=0.

Esto concluye el análisis del diagrama de tiempos mostrado.


PROBLEMA: Analizar el circuito que se muestra a continuación. (Sugerencia: Supóngase que el circuito está inicialmente en el estado Q₁Q₂Q₃=000 y constrúyase una tabla de secuencias para el mismo.)

Este circuito es muy similar a un "registro recirculante", con la diferencia de que las salidas del último flip-flop (en este caso, el flip-flop 3) están invertidas antes de ser conectadas a las entradas del flip-flop al principio de la configuración (el flip-flop 1). La salida Q del tercer flip-flop está conectada a la entrada K del primer flip-flop y la salida Q del tercer flip-flop está conectada a la entrada J del primer flip-flop. Suponiendo que el estado inicial es Q₁Q₂Q₃=000, podemos construír una tabla de secuencias siguiendo la secuencia propiciada por una alimentación de pulsos de "reloj" en la terminal de entrada, tomando a la vez en cuenta el comportamiento de los flip-flops J-K en este tipo de circuito:

Este circuito recibe los nombres de contador de anillo caminante (walking ring counter), contador Johnson (Johnson counter), contador de anillo complementario (complementary ring counter) y anillo de código Grey (Grey code ring), entre otros tantos.


PROBLEMA: El flip-flop D. Los problemas anteriores indican que la mayoría de los circuitos lógicos centrados en la configuración del tipo "registro de transferencia" siempre usan terminales complementarias a la entrada en las terminales J y K de cada flip-flop usado. Considerando esto, ¿qué simplificación se puede hacer con los bloques fundamentales del sistema?

Tomando en cuenta que en este tipo de circuitos se desea que la salida Q de cada flip-flop tome directamente el valor de su entrada J después de cada transición de "1" a "0" en la terminal de "reloj" C, y que para que esto ocurra es indispensable que la alimentación a la terminal K sea el complemento del valor lógico en la terminal J, podemos hacer la siguiente mejora al flip-flop J-K:

Esta configuración se simplifica generalmente encerrándola en una "caja negra" con la siguiente simbología, reteniendo todas sus características originales:

Este bloque representa el elemento conocido comunmente como el flip-flop D; y aunque menos versátil que el flip-flop J-K, requiere de mucho menos conexiones que el flip-flop J-K en una infinidad de circuitos, o sea, ofrece menos problemas de alambrado en la construcción de circuitos lógicos. El flip-flop D es tan útil y tan versátil que se puede adquirir en pares dentro de un circuito integrado de bajo costo como el 4013 (construído con tecnología CMOS, véase el Suplemento # 1: Las familias lógicas):

Las terminales de Set S y de Reset R son para "forzar" a cada flip-flop D a entrar en el estado Q=1 y en el estado Q=0, respectivamente, independientemente del estado en el que se haya encontrado previamente. Un aspecto interesante de la tecnología CMOS usada por este circuito integrado es que el voltaje V_DD de la fuente de poder puede variar desde +3 volts hasta +15 volts, como lo indica el diagrama, y aún así el circuito integrado será capaz de interpretar la presencia o ausencia del mismo como un "1" ó como un "0".

Además del circuito integrado mencionado, tenemos otros como el CD40175 (también fabricado con tecnología CMOS) cuya relación de terminales "pins" en el circuito integrado es la siguiente (obsérvese que la señal de "reloj" o clock puesta en la terminal 9 actúa simultáneamente sobre los cuatro flip-flops D que hay dentro del circuito integrado, lo cual es una gran ayuda para diseños en los que es importante mantener a todos los componentes sincronizados):

o como el circuito integrado CD4175 (también fabricado con tecnología CMOS) cuyo diagrama funcional interno es el siguiente:

Además de ser fabricado con tecnología CMOS, el flip-flop D también ha sido fabricado con tecnología TTL, de lo cual se muestra como ejemplo el circuito integrado octal 74LS374 (el prefijo "74" indica que pertenece a la familia TTL de circuitos lógicos, y el sufijo intermedio "LS" significa Low power Schottky señalando que es de consumo bajo de energía y de alta velocidad):

el cual contiene ocho flip-flops D independientes el uno del otro, excepto por el hecho de que, como puede verse en el diagrama para este circuito integrado, todos los flip-flops D están conectados a la misma terminal de "reloj" designada CK, la cual viene de la terminal 11.


PROBLEMA: Diseñar un registro de transferencia con capacidad de 4 bits, del tipo "entrada serial, salida serial", usando flip-flops D.

Con la entrada designada como "In" y la salida como "Out" tal y como se acostumbra en mucha literatura técnica, el circuito pedido tiene la siguiente configuración:

Este tipo de registro también es conocido en la literatura técnica como registro siso (serial-in serial-out).

La simpleza del diseño en este caso usando flip-flops D en lugar de flip-flops J-K es obvia. La cantidad inferior de alambrado requerido se reflejaría en un circuito impreso como una menor cantidad de líneas requeridas en la tablilla para interconectar los elementos.


PROBLEMA: Diseñar un registro de transferencia con capacidad de 3 bits, del tipo entrada-paralela salida-serial, usando flip-flops D.

Tomando en cuenta que en la entrada paralela se introducen todos los bits de información al mismo tiempo, el diseño en cuestión será como sigue:

La forma en la cual trabaja este circuito es la siguiente: la palabra binaria de entrada de tres bits es colocada en las terminales de entrada B_in(1), B_in(2) y B_in(3). Tras esto, se tiene que activar la terminal que dá la autorización para escribir la palabra dentro del registro, la terminal de escritura W (Write), la cual activa tres bloques AND que sirven como compuertas. Una vez que la terminal W es activada con un "1", se aplica un pulso de reloj con el cual cada uno de los flip-flops D es "cargado" con su bit correspondiente. Hecho esto, se remueve el "1" de la terminal W, con lo cual no entrará información alguna de los AND hacia los flip-flops. Y puesto que la salida Q de cada flip-flop está conectada a la entrada D del que le sigue excepto el tercero por el cual irá saliendo la información en la terminal de salida Out, la aplicación de pulsos sucesivos en la terminal de "reloj" hará que la información avance en forma serial de un flip-flop al siguiente. Este mismo principio de diseño se puede extender hacia un registro de este tipo con cualquier cantidad de flip-flops.

Este tipo de configuración es esencialmente útil en lugares en donde el procesamiento de información se lleva a cabo en forma paralela, manejando varios bits al mismo tiempo en una sola operación. El procesamiento de información en forma paralela es, por regla general, más rápido que el procesamiento de informaciónen forma serial, aunque algo más costoso por el número de componentes adicionales y líneas de conducción eléctrica adicionales que se requieren, según se puede ver comparando la estructura del circuito en este problema con la estructura del circuito del problema anterior.

Un circuito de esta naturaleza es tan útil, que inclusive es puesto a la venta en circuitos integrados comerciales como el CD4014:

fabricado con tecnología CMOS que contiene un registro de transferencia de ocho bits este tipo. Este circuito integrado puede ser utilizado como un registro de transferencia de 6, 7 u 9 etapas, ya sea como un registro de transferencia de entrada serial salida serial, o como uno de entrada paralela salida serial, y se puede conectar en "cascada" para obtener longitudes mayores. Para utilizarlo como un registro de transferencia del tipo entrada paralela salida serial, activamos la terminal "pin" 9 (Par/Ser) con un "1", mientras que para utilizarlo como un registro de transferencia del tipo entrada serial salida serial aterrizamos la misma terminal con un "0". Es importante tomar nota de que en esta misma terminal usada para seleccionar dos modos diferentes de operación, la opción de operación Par se activa poniéndole un "1" a la terminal, mientras que la opción de operación Ser que está complementada se activa poniéndole un "0" a la misma terminal. Esta notación técnica es de uso general. Los datos que van siendo metidos en forma serial por la terminal 11 de entrada (Serial Input) son transferidos por la primera etapa en cada transición positiva (de "0" a "1") de la señal de "reloj" aplicada en la terminal 10 (Clock Pulse). Tras seis pulsos sucesivos de reloj, estos datos comienzan a aparecer en la terminal 2 identificada como "Q6 Output". Un pulso adicional de reloj transfiere los datos para que el último bit llegue a la terminal 12 identificada como "Q7 Output", y otro pulso adicional hace que este último bit aparezca en la terminal 3 identificada como "Q8 Output". Pulsos adicionales de reloj harán que se pierda este bit de información a menos de que los datos sean recirculados o que se conecte la información en "cascada" hacia otro 4014. Para cargar información paralela, se aplica una palabra de ocho bits (un byte) de las terminales Par 1 Input hasta la Par 8 Input, poniendo al bit de Par 1 Input en la cercanía de la entrada al registro y al bit de Par 8 Input en en la cercanía de la salida del mismo. La palabra de entrada paralela es cargada en forma síncrona (todos los ocho bits entran al mismo tiempo) en la transición positiva de la señal de "reloj".

Existe otro tipo de registro de transferencia en el cual la palabra puede ser "cargada" de inmediato sin necesidad de tener que esperar a la aplicación de un pulso de reloj, y ejemplo de ello es el circuito integrado 4021:

también fabricado con tecnología CMOS y también con capacidad de ocho bits.