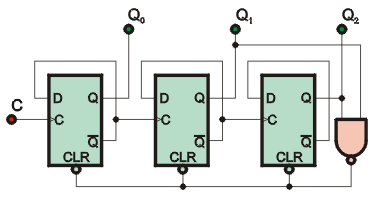
PROBLEMA: Dado el siguiente circuito secuencial asincrono construído a base de flip-flops D:
obtener la tabla de secuencias para dicho circuito suponiendo que los flip-flops D utilizados son del tipo en los cuales los cambios de estado ocurren en la transición positiva (de "0" a "1") del pulso a la entrada de la terminal de reloj. Tras esto, supóngase que hubo una equivocación en la adquisición de los flip-flops D y que el circuito se construye con flip-flops del tipo en los cuales los cambios de estado ocurren en la transición negativa del pulso a la entrada de la terminal de reloj. ¿Qué diferencia hay entre el comportamiento de ambos?
Supondremos, como de costumbre, que el estado inicial del circuito es Q0Q1Q2=000.
Al empezar, para la primera transición, con dos ceros en el NAND, Q1Q2=00; esto pone un "1" en su salida, el cual es invertido en la burbuja inversora NOT en la terminal Clear (CLR) de los tres flip-flops D y por lo tanto no afecta a ninguno de ellos. El primer flip-flop D cambia de estado de Q0=0 a Q0=1 por estar alimentada su entrada con su salida complementaria Q0=1 (de hecho, el primer flip-flop se estará comportando todo el tiempo como un flip-flop T). Este cambio hace que Q0 caiga de "1" a "0" , sin efecto alguno en el segundo flip-flop que le sigue puesto que sólo las transiciones de "0" a "1" en la terminal C producirán un cambio. Por lo tanto, el segundo flip-flop se queda en su estado Q1=0, y lo mismo sucede con el tercer flip-flop.
Para la segunda transición de estados, el primer flip-flop, siempre alimentado en su entrada D con su salida complementaria Q0, cambia su salida de Q0=1 a Q0=0. Pero el segundo flip-flop, estando alimentado con Q0, ve cambiar esta terminal de Q0=0 a Q0=1, con lo cual se provoca un cambio de estado en el segundo flip-flop.
Manteniendo un análisis semejante, acumulamos la siguiente información.
Primera transición: El estado es Q0Q1Q2=100.
Segunda transición: El estado es Q0Q1Q2=0100.
Tercera transición: El estado es Q0Q1Q2=110.
Cuarta transición: El estado es Q0Q1Q2=001.
Quinta transición: El estado es Q0Q1Q2=101.
Al llegar a la sexta transición, tenemos la situación Q1Q2=11, lo cual hace que la salida del NAND cambie de "1" a "0", y este "0" al ser invertido por las burbujas inversoras NOT en las terminales CLR de los tres flip-flops "limpia" al circuito regresándolo al estado Q0Q1Q2=000. Esto se ve más claramente en el diagrama de tiempos para este circuito:
Todo el comportamiento del circuito se puede resumir entonces en la siguiente tabla de secuencias:
El circuito es pues un contador asíncrono módulo 6.
Ahora llevaremos a cabo el análisis sobre este mismo circuito suponiendo que fue construído con flip-flops D cuyo cambio de estado ocurre durante la transición negativa en la terminal de reloj C.
Suponiendo que el estado inicial es Q0Q1Q2=000, al llevarse a cabo la primera transición de "1" a "0" en la terminal C del primer flip-flop. Antes de que ocurra la transición, con dos ceros a la entrada del NAND por el hecho de que Q1Q2=00, hay un "1" a la salida del mismo, el cual es invertido a un "0" por la burbuja inversora NOT en la terminal CLR de los tres flip-flops D. Al ocurrir la transición, el primer flip-flop D cambia de estado de Q0=0 a Q0=0 por estar alimentada su entrada D con su salida complementaria Q0=1. Lo mismo ocurre con el segundo flip-flop por caer su entrada de reloj C de "1" a "0 al cambiar Q0 de "1" a "0". Y lo mismo ocurre en el tercer flip-flop. Pero esto hace que Q1Q2=11, lo cual a la salida del NAND produce un "0", el cual es invertido por cada burbuja inversora NOT a "1" en todas las terminales CLR, "limpiando" el circuito regresándolo al estado Q0Q1Q2=000. Este circuito jamás saldrá del estado Q0Q1Q2=000. Por el simple hecho de haberse utilizado flip-flops activados por transiciones negativas en vez de flip-flops activados por transiciones positivas, el contador modulo 6 ha quedado totalmente inutilizado.
Por regla general, cuando un circuito secuencial asíncrono ha sido diseñado para cambiar de estados con transiciones positivas en la terminal de reloj, si se utilizan flip-flops cuyo cambio de estados ocurre con transiciones negativas el comportamiento del circuito será totalmente diferente e impredecible. Y viceversa.
Es posible modificar el segundo circuito para que se comporte igual que el primero, pero ello requiere poner un inversor NOT conectado inmediatamente a la entrada de cada terminal de reloj C de todos los flip-flops. Si el circuito hubiese sido síncrono, solo se hubiera requerido poner un solo NOT inversor a la entrada de la terminal de reloj "maestra" para igualar los comportamientos de ambos circuitos.
PROBLEMA: Obtener la tabla de secuencias producida por el siguiente contador:
suponiendo que los flip-flops J-K utilizados son activados en sus cambios de estado por una transición positiva (de "0" a "1") en su terminal de "reloj", pero suponiendo también que la combinación de valores J=0 y K=0 se mantiene como la combinación que hace que el flip-flop J-K cambie de estado cada vez que hay una transición positiva en la terminal de "reloj". Supóngase que el estado inicial del contador es Q3Q2Q1=000.
Suponiendo que el estado inicial del contador es Q3Q2Q1=000, al ir la terminal de entrada de "0" a "1" el primer flip-flop cambiará de estado de Q1=0 a Q1=1. Pero como la salida del primer flip-flop está alimentando la terminal de entrada C del segundo flip-flop, al ir de "0" a "1" esto cambiará el estado del segundo flip-flop de Q2=0 a Q2=1. Y como la salida del segundo flip-flop está alimentando la terminal de entrada C del tercer flip-flop, al ir de "0" a "1" el tercer flip-flop cambiará de estado de Q3=0 a Q3=1 . Todo el contador pasará del estado Q=Q3Q2Q1=000 al estado Q3Q2Q1=111. Al siguiente pulso de "reloj" en la terminal principal de entrada C, únicamente cambiará el estado del primer flip-flop pasando de Q1=1 a Q1=0, lo cual no tendrá efecto alguno sobre el segundo flip-flop y a su vez tampoco producirá efecto alguno en el tercer flip-flop. El contador pasa pues del estado Q3Q2Q1=111 al estado Q3Q2Q1=110. Al siguiente pulso, el primer flip-flop cambia de estado de Q1=0 a Q1=1, lo cual cambiará el estado del segundo flip-flop de Q2=1 a Q2=0, lo cual no tendrá efecto alguno sobre el tercer flip-flop. Así, el contador pasará del estado Q3Q2Q1=110 al estado Q3Q2Q1=101. Repitiendo el análisis, logramos obtener la siguiente tabla de secuencias:
No nos debe llevar mucho tiempo para reconocer en base a esta tabla de secuencias que este contador es un contador binario de conteo descendente, un contador binario que va contando "hacia abajo" en lugar de ir contando "hacia arriba". Pero si repasamos los problemas anteriores, encontraremos uno en el cual estudiamos precisamente este mismo circuito, excepto que en dicho problema se comportaba como un contador binario de conteo ascendente. El giro radical en el comportamiento del circuito se dió porque en vez de utilizar flip-flops J-K en los cuales el cambio de estado ocurre cuando la transición en la terminal de reloj es una transición negativa utilizamos ahora flip-flops J-K en los cuales la transición positiva en la terminal de reloj C es la que produce el cambio de estado. Al llevar a cabo un diseño, la especificación de los flip-flops a ser utilizados, ya sea flip-flops activados por una transición negativa o flip-flops activados por una transición positiva, se vuelve tan importane como el diseño mismo, ya que cualquier ambigüedad en dejar clara esta especificación puede arruinar el propósito del diseño produciendo un circuito secuencial con un comportamiento que puede ser completamente inesperado.
PROBLEMA: El siguiente contador es capaz de comportarse de dos maneras diferentes dependiendo del valor que esté puesto en la terminal X. Obténganse las tablas de secuencias tanto para X=1 como para X=0, suponiendo que los elementos flip-flops J-K son del tipo en los cuales el cambio de estados ocurre para una transición negativa en la terminal de reloj C. Se sobreentiende que las terminales J y K están activadas todo el tiempo con los valores que deben tener, no mostrados en el diagrama esquemático, para que se produzca un cambio de estado en cada transición. ¿Qué se puede deducir de los resultados obtenidos y de la comparación de las tablas?
Obviamente, este es un contador asíncrono.
Este circuito es interesante porque los dos NANDs que alimentan a la entrada C del cuarto flip-flop J-K tienen sus salidas conectadas a directamente al mismo punto, lo cual anteriormente se ha dicho que es algo impropio en la conexión de bloques lógicos. Sin embargo, en este caso tal situación es permisible porque los flip-flops que están siendo utilizados son los conocidos comunmente como de lógica de colector abierto (open collector logic), lo cual indica que si la salida de cualquiera de los dos NANDs es "0", entonces dicha salida "jalará" toda la juntura al estado "0" sin importar el valor que esté tratando de poner a su salida el otro NAND, ejecutándose implícitamente la acciónAND por la lógica del colector abierto (repasar el texto principal del segundo capítulo, "Las tres funciones lógicas básicas").
Como el diagrama esquemático no muestra que las entradas J y K de cada flip-flop estén condicionadas de alguna manera, podemos suponer que están puestas a un valor tal que cada transición negativa en la terminal de "reloj" C hará que cada flip-flop cambie de estado, ya que de lo contrario para las otras combinaciones de valores binarios en J y K el circuito no haría absolutamente nada útil.
Empezaremos suponiendo que este contador está en el estado QAQBQCQD=0000. Si la terminal X tiene puesto un valor de "0" todo el tiempo, entonces al empezar todos los componentes lógicos utilizados en el contador tendrán los siguientes valores a sus entradas y sus salidas:
Al ocurrir la primera transición, al ir la terminal "Clock" de "1" a "0", el primer flip-flop situado en el extremo izquierdo cambiará su estado de QA=0 a QA=1. Esto hará que la salida del AND superior alimentado por QA tome un valor de "1", el cual al alimentar al primer NOR en el extremo izquierdo hará que la salida de dicho NOR tome un valor de "0". Con esto, la entrada C del segundo flip-flop caerá de "1" a "0", haciendo que el segundo flip-flop J-K también cambie de estado de Q=0 a Q=1, y a través del segundo AND alimentado por QB que toma el valor de "1" el segundo NOR también pondrá una salida de "0" haciendo que la terminal C del tercer flip-flop cambie de "1" a "0", con lo cual la salida del tercer flip-flop cambiará de QC=1 a QC=0.
En lo que respecta al cuarto flip-flop, este tiene conectadas a su entrada las salidas de dos NANDs, lo cual es posible únicamente bajo la "lógica de colector abierto" ó "lógica alambrada", con lo cual las salidas de los dos NANDs es puesta efectivamente en una función lógica AND; si cualquiera de las salidas de los dos NAND es cero dicha salida "jalará" la salida combinada de ambos NAND a "0". Al cambiar la salida del tercer flip-flop de QC=1 a QC=0, la salida del NAND superior cambiaría de "1" a "0", y por la lógica del colector abierto este "0" jalará el "1" que está poniendo a su salida el segundo NAND, con lo cual la entrada C del cuarto flip-flop cambia de "1" a "0" haciendo que el cuarto flip-flop cambie de estado de QD=0 a QD=1.
De este modo, tras la primera transición, el contador está en el estado QAQBQCQD=1111, lo cual hace que los componentes que todos los componentes lógicos utilizados en el contador tengan los siguientes valores a sus entradas y sus salidas:
Repitiendo el análisis llevado a cabo anteriormente, resulta fácil determinar que, con estos valores, el siguiente estado del contador, su tercer estado, al cambiar la entrada "Clock" al primer flip-flop de "1" a "0" cambiando su salida de QA=1 a QA=0, será QAQBQCQD=0111, por el simple hecho de que en esta ocasión la salida del primer flip-flop asciende de "0" a "1" haciendo con ello que la salida del primer NOR cambie de "0" a "1", y las transiciones positivas en la terminal C (en este caso la del segundo flip-flop) no producen cambios de estado. En pocas palabras, el cambio que experimenta el primer flip-flop no se "propaga" de izquiera a derecha a todos los flip-flops restantes como ocurrió en la situación anterior. Sin embargo, en la siguiente transición, pasando al cuarto estado, tanto el primer flip-flop como el segundo flip-flop cambiarán, pasando el contador al estado QAQBQCQD=1011. Continuando el análisis como lo hemos hecho, podemos ver que para X=0 la tabla de secuencias para el contador empezando con el estado QAQBQCQD=1111 será la siguiente:
No nos debe llevar mucho tiempo el darnos cuenta de que lo que tenemos aquí es un contador binario descendente, ejecutando un conteo binario descensivo desde "1111" hasta "0000". Esto, para X=0.
Veamos ahora lo que ocurre para X=1.
En este caso, suponiendo nuevamente que el contador está en el estado QAQBQCQD=0000, si la entrada X tiene puesto un valor de "1" todo el tiempo, entonces al empezar todos los componentes lógicos utilizados en el contador tendrán los siguientes valores a sus entradas y sus salidas:
Al ocurrir la primera transición, al ir la terminal "Clock" de "1" a "0", el primer flip-flop situado en el extremo izquierdo cambiará su estado de QA=0 a QA=1. Pero este cambio ya no se verá reflejado en los flip-flops posteriores en virtud de que una de las entradas del AND superior conectado al primer flip-flop tiene puesto un valor permanente de "0" todo el tiempo, el "0" proveniente de la entrada X, lo cual tiene el efecto de sacar a la salida QA del primer flip-flop de la acción. Será ahora la salida complementaria QA la que determine lo que ocurre. En la primera transición, esta terminal complementaria cambia de QA=1 a QA=0, haciendo que la salida del NOR cambie de "0" a "1", haciendo que la entrada a la terminal C del segundo flip-flop suba también de "0" a "1", lo cual no producirá transición en el segundo flip-flop. De este modo, tras la primera transición el contador estará en el estado QAQBQCQD=1000. Y en la segunda transición, el contador pasará al estado QAQBQCQD=0100. Continuando el análisis como lo hemos hecho, podemos ver que para X=1 la tabla de secuencias para el contador empezando con el estado QAQBQCQD=0000 será la siguiente:
De la tabla de secuencias nos debe quedar claro que lo que tenemos aquí es un contador binario ascendente, ejecutando un conteo binario ascendente desde "0000" hasta "1111". Esto, para X=0.
Las tablas de secuencias nos han revelado de inmediato que siendo el contador un contador binario de conteo ascendente para X=1, y un contador binario de conteo descendente para X=0, lo que tenemos es, en efecto, un contador dual, el equivalente de dos contadores en uno solo, y todo lo que tenemos que hacer para cambiar el comportamiento es poner un "1" o un "0" en la terminal X.
Ahora nos debe ser obvio que la terminal X, dependiendo del valor que tome, sacará de la acción a los ANDs inferiores (X=0) y meterá dentro de la acción a los ANDs superiores, o bien meterá dentro de la acción a los ANDs inferiores (X=1) y sacará de la acción a los ANDs superiores. Este es a fin de cuentas el propósito de la terminal X y el inversor lógico proporcionado por el NAND de una entrada: meter una hilera de salidas Q dentro de la acción sacando fuera cualquier efecto que pudieran tener las salidas complementarias Q, o bien meter una hilera de salidas complementarias Q dentro de la acción sacando fuera cualquier efecto que pudieran tener las salidas Q. Esta es una estrategia general de diseño válida cuando queremos tener un circuito secuencial dual que sea capaz de comportarse de dos maneras diferentes. Y de hecho, podemos extender el concepto para construír un circuito secuencial que pueda comportarse de tres maneras diferentes, o de cuatro maneras diferentes, o de más maneras diferentes. Esta es la base para un circuito secuencial generalizado cuyo comportamiento puede ser determinado por varias entradas. Este es el principio básico de un autómata determinístico implementado por completo por la vía del "hardware" mediante circuitos integrados que posean funciones lógicas básicas.
Exponsor
CURSO TÉCNICO INSTALADOR DE ENERGÍA SOLAR TÉRMICA
Visita el siguiente enlace: http://enersolartermica.blogspot.com.es/
¡No pierdas esta magnifica oportunidad de poder formarte en esta profesión con gran demanda de empleo!
Ahora por oferta de lanzamiento y por tiempo limitado puedes adquirir este curso por solo 9,95€, cuando su valor de mercado es de 49€.
Suscribirse a:
Enviar comentarios (Atom)










No hay comentarios:
Publicar un comentario