Para lograr una reducción del número de líneas requeridas, modificamos el ROM del problema anterior añadiendo compuertas a la salida de información de cada columna para así tener la siguiente configuración (cada una de las compuertas está mostrada de color amarillo, y en cada una de ellas es necesario poner un "1" en cada terminal C para permitir el flujo de la información a través de la compuerta):
El circuito anterior frecuentemente se simplifica de la siguiente manera:
En este caso, se escogió la salida producida cuando la letra B ha sido seleccionada. El indicador alfanumérico luminoso presentará el siguiente aspecto (los puntos LED no activados correspondientes a la letra B están distinguidos con color amarillo pálido) cuando la columna 3 de la matriz está siendo activada (los puntos LED correspondientes a la columna activada están distinguidos con color rojo):
Antes que nada, se puede observar que un ROM que poseía originalmente 35 terminales de salida posee únicamente 7 a cambio de añadir 5 terminales de entrada (las correspondientes a los selectores de columnas Ci). ¡Este es un ahorro substancial de alambrado! De la misma manera, el indicador luminoso que requería 35 terminales de entrada requiere ahora únicamente de 12. Para representar un caracter ASCII bajo esta técnica (después de que ha sido seleccionado en la sección de domicilios del ROM) se va activando cada una de las terminales Ci sucesivamente tanto en el ROM como en el indicador, con la suficiente rapidez para que bajo el fenómeno conocido como la persistencia visual (que ha hecho posible la televisión y la cinematografía) el indicador dé la impresión de estar representando un caracter fijo e inmóvil, aunque no sea así. Este método mediante el cual se pueden reducir considerablemente las líneas requeridas para la interconexión de los elementos de un sistema recibe el nombre de multiplex y puede reducir considerablemente la complejidad de los circuitos, según se puede apreciar en este problema.
Es importante agregar que, aún con la técnica del multiplex, el consumo de energía requerido por los indicadores luminosos LED eventualmente los hizo imprácticos para aplicaciones portátiles de bolsillo tales como los relojes de mano (los primeror relojes de mano digitales que aparecieron en el mercado fueron hechos a base de diodos emisores de luz LED, pero estos no daban una indicación continua de la hora todo el tiempo, había que oprimir un botón para que apareciera la lectura en la carátula). Esta es la razón por la cual en muchas aplicaciones portátiles los diodos emisores de luz fueron reemplazados por otra tecnología que requiere un consumo mucho menor de energía por estar basada no en la emisión de luz proveniente de un semiconductor sino en la reflexión y absorción de la luz en base a carátulas de cristal líquido (liquid crystal display ó LCD):
en las cuales la transparencia o la opacidad del punto seleccionado dependerá de la aplicación de un voltaje (un "1"):
y las cuales pueden proporcionar un nivel de detalles bastante aceptable para muchas aplicaciones portátiles, como en la siguiente muestra tomada de la carátula de una cámara digital:
De cualquier modo, y es importante señalarlo, aún las carátulas de cristal líquido utilizan en forma intensiva la técnica del multiplex.
PROBLEMA: Se desea almacenar el número pi (π = 3.141592654) en forma permanente dentro de una calculadora electrónica usando el sistema BCD. Describir las características del ROM utilizado. Ignorar el punto decimal.
Designando al dígito en el extremo izquierdo del número pi (π) como el primero, la Tabla de Verdad indicando el número BCD requerido para cada dígito será como sigue:
Puesto que para representar cada dígito en el sistema BCD se requieren 4 terminales de salida, para leer los diez dígitos se requerirán 40 terminales de salida en el ROM, lo cual representa una cantidad intolerable de alambrado. Usando la técnica del multiplex (MUX) estudiada en un capítulo previo, podemos simplificar el ROM haciendo que la activación de un dígito en particular nos dé a la salida del ROM el número BCD correspondiente a dicho dígito, como se muestra a continuación:
De este modo, al activar la terminal correspondiente al primer dígito, en las cuatro terminales de salida se tendrá el número BCD 0011 correspondiente al dígito 5, con lo cual la salida , equivalente al número decimal 3, el primer dígito del número π. Al activar la terminal correspondiente al segundo dígito, en las cuatro terminales de salida se tendrá el número BCD 0001, equivalente al número decimal 1, el segundo dígito del número π. Es obvio que para sacar el número π del ROM habrá que activar cada terminal "dígito" en una secuencia ordenada y continua. En el diagrama se muestra activada la quinta terminal del ROM con lo cual la salida toma la condición 0101, equivalente al número decimal 5, el quinto dígito del número π.
El número e (= 2.718281828) también se puede almacenar en una calculadora electrónica en forma permanente usando la técnica arriba descrita. Y de hecho, así es como se almacenan los números π y e en una calculadora electrónica de bolsillo, usando una memoria ROM. Por esto las calculadoras de bolsillo nunca olvidan estos dos números célebres.
PROBLEMA: Ocasionalmente, es deseable tener a la mano un ROM cuyo contenido pueda ser programado para alguna aplicación especial en un proyecto particular. Esto se logra diseñando un ROM con fusibles internos, habiendo tantos fusibles como bits usados. Teniendo esto en mente, diseñar un ROM programable de dos entradas y tres salidas.
Puesto que la unidad tiene dos entradas, las combinaciones posibles de "unos" y "ceros" son cuatro, las cuales son procesadas por un decodificador tomando cada combinación y activando a la vez una sola línea a la salida del mismo. El circuito presentará el siguiente aspecto:
Este tipo de ROM programable es conocido comúnmente como la PROM (Programmable Read Only Memory). Para programar un PROM, cada fusible se tiene que hacer estallar individualmente, con un tiempo mínimo de enfriamiento entre cada estallamiento ya que se genera cierta cantidad de calor dentro del circuito.
PROBLEMA: ¿Cuáles serán las palabras binarias de salida producidas por la siguiente memoria PROM que ya ha sido programada y que por lo tanto se puede considerar convertida ya a una memoria ROM?
Es importante recordar que sólo una de las líneas A0, A1 y A2 puede estar activada a la vez. Empezamos por ver que en el primer renglón ninguno de los fusibles-diodos ha sido "quemado", de modo que cuando la línea A0 está poniendo un "1" en el primer renglón ese "1" pasa directamente a las tres columnas D2, D1 y D0 que la cruzan. Entonces la salida será D2D1D0=111 para A0=1. En el segundo renglón, el fusible-diodo intermedio ha sido "quemado" y ya no está presente para pasar a la columna D1 un "1" puesto en el renglón A1. Entonces la salida será D2D1D0=101 para A1=1. Por último, en el tercer renglón, el fusible-diodo alineado con la columna D0 ha sido "quemado" y ya no está presente para pasar a la columna D0 un "1" puesto en el renglón A2. Entonces la salida será D2D1D0=110 para A2=1.
PROBLEMA: ¿Cuáles serán las salidas S1 y S2 producidas por la siguiente memoria en función de las entradas a, b, c y d? ¿De qué tipo de memoria se trata?
En el primer renglón correspondiente a la entrada a, el tercer diodo-fusible de izquierda a derecha ha sido "vaporizado", y por este motivo la línea a no podrá poner nada en la tercera columna cuando la entrada a tenga el valor de "1". Considerando que sólo una de las líneas a, b , c ó d puede estar activada a la vez, al poner un "1" en la línea a
Las dos salidas Boleanas del circuito serán por lo tanto:
S1 = ab + bc
S2 = ac + abd
S2 = ac + abd
No resulta difícil ver que esta memoria consta de dos matrices, la primera es la matriz superior que está atravesada por las líneas (renglones) a, b, c y d, mientras que la segunda matriz es la matriz inferior que está atravesada por las líneas (renglones) S1 y S2. Y ya vimos que tanto en la matriz superior como en la matriz inferior se "quemaron" varios fusibles, lo cual significa que tanto las entradas como las salidas son programables. Entonces la memoria es un PLA.
PROBLEMA: ¿Qué es una línea de retardo?
Considérese la siguiente configuración:
Aparentemente, la combinación arriba mostrada no lleva a cabo ninguna función útil, ya que la información que es invertida por el primer inversor vuelve a ser invertida por el segundo inversor obteniéndose así a la salida la información original a la entrada sin cambio alguno.
Sin embargo, un momento de reflexión nos indica que tenemos a la mano una variable que no habíamos considerado hasta ahora. Sabemos de antemano que al introducir información binaria a la entrada de un inversor, es físicamente imposible que aparezca instantáneamente la respuesta a la salida del mismo. En efecto, antes de llegar al límite impuesto por la velocidad de la luz, entran en juego otros parámetros físicos relacionados con las cuestiones eléctricas (tales como la inductancia y la capacitancia) que ponen un límite a la velocidad de respuesta del inversor. Esto es, hay un retardo de tiempo introducido por el inversor. Dependiendo de la familia lógica utilizada (véase el Suplemento # 1: Las familias lógicas), cada circuito integrado tendrá un retardo en la propagación de la señal desde su entrada hasta su salida conocido en las especificaciones técnicas como retardo de propagación (propagation delay). A manera de ejemplo, para un inversor NOT disponible en un circuito integrado TTL 7404, el retardo de propagación en promedio es de 10 nanosegundos, y para un inversor NOT disponible en un circuito integrado CMOS 4049 el retardo de propagación en promedio es de 25 nanosegundos. Hasta ahora se había considerado este retardo de tiempo como despreciable. Sin embargo, al conectar dos inversores en serie, este retardo de tiempo se vuelve el doble del retardo original.
Configuraciones como la anterior que no llevan a cabo ningún procesamiento de información pero que introducen un retardo de tiempo T a la información a su entrada se conocen comúnmente como línea de retardo y se pueden representar de la siguiente manera:
La doble banda indica el lado en el cual se introduce la información en la línea de retardo. El retardo de tiempo T se indica dentro de la línea de retardo (100 microsegundos, 10 nanosegundos, etc.).
Básicamente, el funcionamiento es sencillo. Si se introduce un "1" a la entrada de la línea de retardo, después de un tiempo T aparecerá un "1" a la salida de la misma. Y si se introduce un "0" en la línea de retardo, después de un tiempo T aparecerá un "0" a la salida de la misma.
Además de los retardos inherentes en los circuitos integrados utilizados para construír sistemas digitales, existen varias formas de obtener retardos de tiempo en la propagación de una señal introduciendo un mínimo de distorsión en la misma, tales como el uso de bobinas como la que se muestra a continuación capaz de producir un retardo de 390 nanosegundos:
Y a continuación tenemos la línea de retardo ADL CS344 que puede producir un retardo constante de 64 microsegundos:
Es muy importante aclarar antes de continuar adelante que las líneas de retardo tienen poco uso en la construcción de sistemas digitales de uso común, excepto para aplicaciones muy especializadas. La línea de retardo es útil en el estudio conceptual de los multivibradores que se pueden construír utilizando circuitos lógicos, y un retardo puede ser producido de modo mucho más económico utilizando una resistencia R y un condensador C cuya constante de tiempo RC en combinación con un temporizador (timer) como el 555 (véase el Suplemento # 8: El temporizador 555) puede ser utilizada para construír multivibradores de todo tipo.
Normalmente, los retardos de tiempo son un efecto sumamente desagradable que los ingenieros de diseño tratan de reducir al mínimo con el fin de tratar de obtener la máxima velocidad posible de un sistema digital (el mejor ejemplo que se puede citar son las computadoras personales de escritorio, cuyas velocidades de procesamiento están limitadas precisamente por estos retardos de tiempo). Sin embargo, para construír los multivibradores que serán tratados en los siguientes problemas, la introducción de retardos de tiempo se vuelve prácticamente una necesidad.
PROBLEMA: Diseñar un multivibrador mono-estable utilizando un flip-flop R-S y una línea de retardo.
El diseño deseado se muestra a continuación:
Para analizar este diseño, suponemos que el flip-flop R-S está inicialmente en la condición R=0, S=0 y Q=0.
Al aplicar un pulso (o un "1") de corta duración en la terminal "gatillo" (trigger), el flip-flop R-S entra en el estado Q=1 en donde permanece después de desaparecer el pulso. Al tomar la terminal de "Salida" el valor Q=1, se coloca al mismo tiempo un "1" a la entrada de la línea de retardo. Transcurrido un tiempo T, este "1" aparece a la salida de la línea de retardo, lo cual a su vez hace que R=1. Puesto que el pulso en la terminal "gatillo" fue de corta duración, al tomar R el valor de "1" encontramos que S ya tiene el valor "0". Con la condición R=1 y S=0, el flip-flop R-S regresa automáticamente al estado Q=0. Este estado Q=0 pone un "0" en la línea de retardo que después de un tiempo T vuelve a dejar al flip-flop R-S en su estado original R=0, S=0 y Q=0.
Un diagrama de tiempos ilustrando la acción sería como el siguiente:
Nótese que el ancho de pulso de la señal "gatillo" siempre debe ser menor que el ancho de la señal de salida para evitar poner al flip-flop en el estado no-definido R=1 y S=1.
El multivibrador monoestable también es conocido como el "multivibrador de un disparo" (one-shot).
PROBLEMA: A continuación se muestran las características de un elemento conocido como el "medio-monoestable":
Según se puede observar, la característica fundamental del medio-monoestable es que el ancho de pulso a la salida tiene una duración menor que el ancho de pulso a la entrada. Tomando en cuenta lo anterior, diseñar un medio-monoestable.
Un diseño posible es el siguiente:
Supongamos que la terminal "gatillo" está inicialmente en la condición "0". La salida de la línea de retardo será también "0" al estar siendo alimentada con el "0" del "gatillo", lo cual producirá un "1" a la salida del inversor. Las entradas del AND serán por lo tanto "1" y "0".
Al aplicar un "1" a la terminal "gatillo", las dos entradas al AND serán "1" y la salida de la configuración tomará el valor de "1".
Transcurrido un tiempo T, el "1" a la entrada de la línea de retardo aparecerá a la salida del mismo, produciendo a su vez un "0" a la salida del inversor. Las entradas al AND serán entonces "0" y "1", con lo cual la salida del AND tomará el valor de "0".
Nótese que para obtener otro pulso de duración T a la salida del medio-monoestable, es necesario regresar la terminal "gatillo" a la condición "0", para así poder estar en condiciones de volver a "disparar" el medio-monoestable.
PROBLEMA: Analizar el comportamiento del siguiente circuito:
Suponemos que la salida es inicialmente Q=0. Esto a su vez implica que S=0 y R=1, considerando que las entradas al flip-flop R-S son complementarias debido a la acción del inversor. Tenemos entonces que Q=1, lo cual pone un "1" a la entrada de la línea de retardo.
Transcurrido un tiempo T, el "1" a la entrada de la línea de retardo aparece a la salida del mismo, lo cual produce las condiciones S=1 y R=0. Esto ocasiona que el flip-flop R-S cambie al estado Q=1.
Al tomar el flip-flop R-S el estado Q=1, entonces Q=0, lo cual pone un "0" a la entrada de la línea de retardo. Transcurrido un tiempo T, el "0" a la entrada de la línea de retardo aparece a la salida del mismo, lo cual produce las condiciones S=0 y R=1. Esto ocasiona que el flip-flop R-S regrese al estado Q=0.
Este proceso se repite indefinidamente.
Notamos, por lo tanto, que el circuito tiene dos estados inestables, Q=0 y Q=1.
Este circuito es básicamente un multivibrador astable de salida simétrica. La característica más interesante de esta configuración que la distingue de todas las demás estudiadas en esta obra es que no tiene entradas. Solo tiene una salida. En efecto, este es un bloque autosuficiente que puede generar por sí solo un tren de pulsos para su uso subsecuente en circuitos lógicos. La salida del mismo tendrá el siguiente aspecto en un diagrama de tiempos:
Podemos ver que el período de la onda será 2T y que la frecuencia de la misma será f=1/2T.
PROBLEMA: Supóngase que a la entrada de la siguiente configuración se introduce un pulso con una duración de tiempo t=T/2. Obtener los diagramas de tiempo de las salidas A, B y C con respecto al pulso de entrada.
Los diagramas pedidos se muestran a continuación:
Al introducir un pulso de duración t en la terminal de entrada, éste aparece en la terminal A después de transcurrido un tiempo T marcado por la línea de retardo. A la vez, este pulso es introducido en la segunda línea de retardo. Transcurrido otro tiempo T aparecerá en la terminal B. Después de haber transcurrido otro tiempo T, el pulso aparecerá finalmente en la terminal C.
Esta configuración en la cual se produce una sucesión de pulsos en terminales consecutivas, ocurriendo únicamente un pulso a la vez, es conocida como Contador de Anillo y desempeña un papel importante en el diseño de computadoras digitales.
Obsérvese que si inmediatamente después de haber introducido el pulso a la entrada de la configuración se conecta la terminal C a la terminal de entrada, esta puede trabajar por sí sola produciendo pulsos por tiempo indefinido. Tenemos entonces lo que se llama un Oscilador de Anillo.
Aunque el diseño de un Contador de Anillo basado en el uso de líneas de retardo teóricamente puede funcionar, en la práctica esto se consideraría como un diseño pésimo, ya que no hay forma de ejercitar algún tipo de control sobre el deterioro que vaya teniendo el pulso como tampoco hay forma de garantizar un control preciso de los tiempos predichos teóricamente. Un Contador de Anillo mucho más confiable y seguro sería aquél cuyo diseño esté basado en bloques lógicos secuenciales bajo la acción directa de la señal de un pulso de reloj maestro, tales como los que serán tratados precisamente en el siguiente capítulo.
PROBLEMA: ¿Cuáles son los problemas potenciales que puede ocasionar en un circuito lógico construído con una variedad de funciones lógicas la presencia de un retardo de tiempo inherente en la respuesta de cada una de las funciones lógicas empleadas?
Considérese el siguiente circuito:
Si este circuito fuera un circuito ideal, sin retardos de tiempo en ninguno de los componentes,
entonces su comportamiento sería sencillo: con una entrada de "0" la salida del mismo debe ser
"0", y al ponerle una entrada de "1" su salida debe seguir siendo "0". Teóricamente, este circuito no debe producir salida alguna cualesquiera que sea el valor a su entrada. Sin embargo, la situación cambia cuando consideramos el retardo de propagación introducido por el bloque NOT, denominado en el diagrama como Δt1. La señal a la salida del NOT no cae instantáneamente de "1" a "0" cuando la entrada A toma el valor de "1". Esto ocasiona que por un lapso breve de tiempo la salida del AND no será "0" sino "1", manifestado como un pulso. El bloque AND introduce su propio retardo de tiempo Δt2 en dicho pulso, de modo tal que el pulso aparecerá a la salida del mismo un tiempo Δt1+Δt2 después. El problema es que dicho pulso, no anticipado y no deseado, puede introducir efectos erráticos inesperados en lo que de otra manera sería un buen diseño. El problema se origina en el hecho de que por el retardo de tiempo introducido por el NOT, se origina una carrera (race) entre las dos señales A y A que llegan a las dos entradas del AND, lo cual a su vez crea una condición de riesgo inesperado (hazard) por la presencia del pulso no-deseado.
En el siguiente diagrama en el cual utilizamos un NOR en lugar de un AND tenemos una condición similar en la cual la duración del pulso no-deseado es mayor aún por el efecto combinado de tres NOTs (actuando como una línea de retardo) conectados en cascada uno tras el otro, triplicando el retardo de propagación introducido por cada uno de ellos:
El siguiente circuito muestra una condición aún más seria:
Primero llevaremos a cabo un análisis estático, sin consideración alguna del factor tiempo.
Supóngase primero que este es un circuito lógico ideal sin retardo alguno en la propagación de la señal a través de cada NOT. Supóngase ahora que la salida del último NOT (en el extremo derecho) es de "0". Esto pone un "0" a la entrada del primer NOT (en el extremo izquierdo), el cual "instantáneamente" es puesto a su salida como un "1", el cual entra al segundo NOT y sale del mismo también "instantáneamente" como un "0". Este "0" es invertido por el tercer NOT y sale del mismo como un "1". Pero habíamos supuesto que la salida del tercer NOT era "0". Claramente esta es una condición incompatible.
¿Entonces qué es lo que sucedería si tratáramos de construír este circuito?
En este caso, no tenemos necesidad de preocuparnos por la situación teórica ideal (la cual trasladada al terreno de las matemáticas puras y al terreno de la lógica nos conduce a una paradoja), porque al momento de construír este circuito lo tenemos que hacer necesariamente con componentes físicos reales, los cuales siempre tienen un retardo de tiempo en la propagación de la señal desde su entrada hasta su salida.
Ahora llevaremos a cabo un análisis dinámico tomando en cuenta lo que va ocurriendo conforme el tiempo va avanzando.
Supóngase que el retardo de propagación en todos los NOTs tiene una duración de un tiempo T. Nuevamente, supóngase que la señal a la salida del tercer NOT es "0" al inicio de un intervalo de un primer tiempo que llamaremos t1, el cual será de duración T. Esta salida de "0" estará también puesta en la entrada del primer NOT (suponemos que el tiempo de viaje de la señal a través del alambre conector del tercer AND al primer AND es despreciable en comparación con el tiempo de propagación de la señal a través de cada NOT), y después de un tiempo T (al finalizar el tiempo t1) este "0" aparecerá a la salida del primer NOT invertido como "1". Al finalizar el primer tiempo t1, también el tercer NOT cambiará su salida a lo que tenía puesto a su entrada. Supóngase que tenía puesto un "1", lo cual a su vez implica que la salida del segundo NOT era "1". Supóngase también que la entrada del segundo NOT era "1". Esto no posible de concebir para un NOT ideal, sin embargo, no es imposible para el caso de un NOT real porque si el segundo NOT tenía un "1" a su salida por haber tenido puesto un "0" previamente a su entrada, entonces al serle puesto un "1" a su entrada su salida no caerá de "1" a "0" hasta que no haya transcurrido un tiempo T. Así el segundo NOT, por considerar que tiene una entrada de "1" y una salida de "1", se encuentra en una condición lógicamente anómala. Sobre estas consideraciones, al inicio del tiempo t1 la situación es la siguiente:
Al finalizar el tiempo t1 y comenzar el tiempo t2, transcurrido un tiempo T, el "0" puesto a la entrada del primer NOT pasa invertido a su salida como un "1". Por otro lado, el "1" puesto a la entrada del segundo NOT pasa invertido a su salida como un "0", con lo cual el segundo NOT deja de estar en una condición lógicamente anómala. Este "0" a la salida del segundo NOT es puesto de inmediato a la entrada del tercer NOT. Por su parte, el "1" que estaba puesto a la entrada del tercer NOT pasa invertido a su salida como un "0", manteniéndose por lo tanto el tercer NOT sin cambio en su condición lógica. Pero esto pone ahora al tercer NOT en una condición lógicamente anómala, al tener un"0" en su entrada y un "0" en su salida:
Al finalizar el tiempo t2 y comenzar el tiempo t3, transcurrido un tiempo T, el "0" puesto a la entrada del primer NOT pasa invertido a su salida como un "1". Por otro lado, el "1" puesto a la entrada del segundo NOT pasa invertido a su salida como un "0", manteniéndose por lo tanto el segundo NOT sin cambio en su condición lógica. Por su parte, el "0" que estaba puesto a la entrada del tercer NOT pasa invertido a su salida como un "1", con lo cual el segundo NOT deja de estar en una condición lógicamente anómala. Pero el "1" que está ahora a la salida del tercer NOT es puesto de inmediato a la entrada del primer NOT, el cual tiene con esto un "1" tanto en su entrada como en su salida. Esto pone ahora al primer NOT en una condición lógicamente anómala:
Al finalizar el tiempo t3 y comenzar el tiempo t4, transcurrido un tiempo T, el "1" puesto a la entrada del primer NOT pasa invertido a su salida como un "0". Por otro lado, el "0" puesto a la entrada del tercer NOT pasa invertido a su salida como un "1", manteniéndose por lo tanto el tercer NOT sin cambio alguno en su condición lógica. Este "1" a la salida del tercer NOT está puesto en la entrada del primer NOT, con lo cual el primer NOT deja de estar en una condición lógicamente anómala al tener una entrada de "1" y una salida de "0". Pero el "1" que estaba puesto a la entrada del segundo NOT pasa ahora a su salida como "0". Al tener una salida de "0" y al tener como entrada el "0" que le está poniendo el primer NOT, el segundo NOT entra ahora en una condición lógicamente anómala:
Si repetimos el análisis considerando que por los retardos de propagación siempre podemos tener temporalmente alguno de los NOTs con un "1" en la entrada y un "1" en la salida, o bien con un "0" en la entrada y un "0" en la salida, una condición lógicamente anómala que está siendo transferida de un NOT a otro sin parar, llegaremos a la conclusión de que el circuito está oscilando:
Y esta es una oscilación errática que está completamente fuera de nuestro control por estar oscilando el sistema en los linderos de condiciones lógicamente incompatibles. Si queremos ejercer algún tipo de control sobre las oscilaciones que se están produciendo, utilizaríamos un AND como medio de control:
Aquí cuando la entrada en la terminal "gatillo" del AND es "0", la salida será siempre "0" independientemente del valor lógico que tenga la otra terminal a su entrada. Esto pone un "0" a la entrada del primer AND, el cual después de un tiempo T pasa invertido como un "1" a su salida, y el cuala su vez después de otro tiempo T pasa invertido como un "0" a la salida del segundo NOT que a su vez después de otro tiempo T pasa invertido como un "1" a la salida del tercer NOT, que queda detenido allí por la acción del AND. La configuración se convierte en una configuración estable. Pero al poner un "1" en la terminal "gatillo" del AND el "1" producido con esto a la salida del AND es puesto de inmediato a la entrada del primer NOT, el cual con el "1" que tenía ya a su salida y con el "1" que le está siendo puesto a su entrada entra en una condición lógicamente anómala, iniciándose así la inestabilidad del sistema.
Curiosamente, si en lugar de haber utilizado tres NOTs conectados en serie retroalimentando la salida del último hacia la entrada del primero, hubiéramos utilizado únicamente dos NOTs, entonces no habríamos tenido oscilación alguna, porque un circuito de este tipo puede poseer dos estados estables que son los siguientes:
Y precisamente por poseer dos estados estables, ninguno de los cuales conduce a una condición lógicamente anómala, este circuito es un circuito biestable (desafortunadamente, su utilidad está limitada por el hecho de carecer de entrada alguna, el estado estable que tome al encender la máquina será totalmente impredecible). Y si conectamos cuatro NOTs en serie, también tendremos dos estados estables. En general, si conectamos un número par de NOTs en serie retroalimentando la salida del último hacia la entrada del primero, siempre tendremos un circuito con dos estados estables. Y si conectamos un número impar de NOTs retroalimentando la salida del último hacia la entrada del primero, tendremos un circuito que estallará en oscilaciones fuera de nuestro control.
El circuito oscilatorio construído a base de tres NOTs es demasiado obvio como para no despertar sospechas dentro de un diseño. En circuitos lógicos sencillos como los que se acaban de mostrar, con un poco de práctica es posible descubrir la posibilidad de que se pueda producir alguna carrera que ocasione un pulso o una serie incontrolable de pulsos no-deseados. Pero en la práctica un sistema digital puede estar formado con cientos o quizá miles de componentes lógicos, lo cual vuelve extremadamente difícil el tratar de descubrir tales condiciones de riesgo inesperado por mera inspección visual del circuito. Inclusive el circuito sencillo que acabamos de ver podría aparecer "disfrazado" en una configuración en la cual en lugar el segundo NOT y el tercer NOT son reemplazados con bloques NOR alimentando a su vez otros componentes lógicos. Si la entrada en las demás terminales de entrada de los NORs se vuelve "0" entonces el esquema se reduce a lo que tenemos arriba, y el sistema estallará en oscilaciones incontrolables no previstas por el diseñista, con un problema sumamente difícil de diagnosticar.
Estas condiciones de riesgo pueden ser minimizadas o eliminadas por completo cuando el comportamiento del sistema está bajo el control de algún reloj maestro, alguna "señal de reloj" (clock) que proporcione un lapso de tiempo suficiente entre una transición de señales binarias distintas para permitir que las cosas se estabilicen, esperando a que estos pulsos que a fin de cuentas son temporales hayan desaparecido. Esta es una de las razones para evolucionar el diseño de los circuitos lógicos hacia una lógica cronometrizada en la cual el flip-flop J-K que será estudiado en un capítulo posterior desempeñará un papel importante. En la práctica, se pueden descubrir este tipo de problemas potenciales en un circuito lógico reproduciendo el circuito en un simulador, un programa de computadora en el que no sólo se aplique a la entrada del circuito todas las combinaciones posibles de "unos" y "ceros" sino que también se introduzca un retardo de tiempo (tomado directamente de las especificaciones técnicas de los componentes utilizados) en cada componente. Los diagramas de tiempo simulados de las salidas lógicas de los circuitos indicarán de inmediato la presencia de estos pulsos que normalmente podrían ser difíciles de predecir y detectar.
PROBLEMA: Cuando un flip-flop R-S es "ajustado" (con la terminal "Set" S) o "reajustado" (con la terminal "Reset" R) el cambio se propaga a las salidas Q y Q del flip-flop dilatado únicamente por los retardos de propagación de los bloques NOR o NAND con los que fue contruído. El problema anterior sugiere la necesidad de ejercer algún control sobre estos cambios para evitar la posibilidad de que en un diseño complicado por efecto de alguna retroalimentación el sistema pueda estallar en oscilaciones inesperadas o ciclar en cambios no anticipados. Para garantizar que el flip-flop R-S (o los flip-flops R-S) cambien su estado en sincronía con otras partes del circuito en donde están siendo utilizados, un buen diseño no les permite cambiar de estado a menos de que hayan recibido una autorización de una señal de "reloj". Bajo esta filosofía, a las terminales R y S no se les permite cambiar la salida Q del flip-flop a menos de que una señal aplicada en una terminal C o CLK llamada "reloj" (clock) tenga un valor "alto" (un valor de "1"). Diseñar un flip-flop R-S que pueda satisfacer estos requerimientos.
Controlar de algún modo lo que entra o lo que sale de cualquier componente o circuito lógico requiere a su nivel más básico el uso de compuertas que bajo el control de una señal lógica de "0" ó "1" detengan o permitan el paso de la información. Esto lo podemos lograr con compuertas formadas con bloques AND, y sería el paso obvio para mejorar el diseño básico de un flip-flop R-S. Si tomamos como punto de partida un flip-flop construído con bloques NAND, podemos agregar una compuerta utilizando también bloques NAND (en vez de usar bloques AND), lo cual tiene la ventaja de que podemos utilizar un bloque que es natural en la microelectrónica de los circuitos integrados. El diseño mejorado será como el que se muestra a continuación:
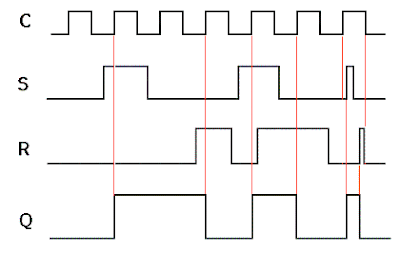
La forma en la cual trabaja este circuito se puede describir mejor con un diagrama de tiempos como el siguiente:
La explicación de este diagrama de tiempos es la siguiente:
Empezamos suponiendo que ambas entradas S y R al flip-flop están en "0", y que la salida del mismo también es Q=0. Al subir la entrada S de "0" a "1", normalmente el flip-flop debería entrar en el estado Q=1; pero no lo hace porque no ha recibido autorización de la señal de "reloj" C para ello. Manteniéndose las entradas en S=1 y R=0, al subir la entrada en la terminal C de "0" a "1" el flip-flop cambia de inmediato su estado de Q=0 a Q=1, porque ya recibió autorización para un cambio de estado. Esto es resaltado por la primera línea roja vertical en el diagrama (a la izquierda). Tras esto y antes del arribo del tercer "pulso" en la terminal C la entrada S cae a "0", reteniendo el flip-flop R-S su valor de Q=1. Al llegar el tercer pulso no ocurre nada porque el flip-flop, en su acción natural, mantiene su estado Q=1. Después de esto, al subir la entrada R de "0" a "1", normalmente el flip-flop debería "reajustarse" al estado Q=0; pero no lo hace porque no ha recibido autorización de la señal de "reloj" C para ello. Manteniéndose las entradas en S=0 y R=1, al subir la entrada en la terminal C de "0" a "1" el flip-flop cambia de inmediato su estado de Q=1 a Q=0, porque ya recibió autorización para un cambio de estado. Esto es resaltado por la segunda línea roja vertical en el diagrama. Después, y antes de que llegue el quinto "pulso de reloj", las entradas son cambiadas a S=1 y R=0, pero el flip-flop mantiene su estado sin cambiar porque el "0" en la terminal C se lo impide. Sólo al inicio del quinto pulso de reloj (resaltado por la tercera línea roja vertical en el diagrama) ocurre la autorización, cambiando la salida de inmediato a Q=1. Tras esto, los valores lógicos en las terminales S y R son cambiados primero a S=1 y R=1 y luego a S=0 y R=1, pero no sucede nada porque aún no llega el sexto pulso de reloj. Pero con estos últimos valores, al llegar el sexto pulso de reloj la salida cae de Q=1 a Q=0, resaltado por la cuarta línea roja vertical en el diagrama. Después viene la caída de "1" a "0" en la terminal R, sin efecto alguno en la salida. Y por último, al llegar el séptimo pulso de reloj, dentro del intervalo que dura el pulso en su condición de "1" ocurren dos "picos" que tienen efectos inmediatos en la salida Q del flip-flop, resaltados por la quinta y la sexta líneas rojas verticales en el diagrama.
Aunque este flip-flop R-S con la terminal de entrada C mostrada representa una mejora sobre el diseño original, el problema con este diseño es precisamente la última condición en la cual pese a que la salida Q del flip-flop NO puede cambiar de estado mientras la terminal C no haya dado su autorización para ello, la salida del flip-flop sí puede cambiar de estado varias veces mientras la terminal C permanezca activada, lo cual requiere algún tipo de correctivo por la vía del rediseño.
Se acostumbra simbolizar este tipo de flip-flop encerrándolo dentro de una "caja negra" como la siguiente:

Podemos interactuar con un flip-flop de este tipo mediante el flip-flop R-S interactivo disponible en la siguiente página:
http://www.play-hookey.com/digital/clocked_rs_latch.html
PROBLEMA: Como se vió en el problema anterior, aún con una terminal de "control" C añadida al flip-flop R-S para, queda el problema de que mientras dicha terminal de entrada esté activada la salida Q del flip-flop estará sujeta a cualquier cambio en el intervalo de tiempo que la entrada C permanezca en un estado que permita cambios en las terminales S y R del flip-flop. En pocas palabras, en vez de cambiar una sola vez cuando la terminal de control dá su autorización para ello, el flip-flop puede cambiar de estado varias veces. ¿Se puede mejorar un diseño de este tipo?
Existe una mejora adicional que se puede implementar al diseño, la cual consiste en permitir cambios en el flip-flop R-S no simplemente cuando la señal de "reloj" C esté alta en "1" (o baja, en "0", según sea el caso) sino únicamente cuando la señal en la terminal de control C está transitando de "0" a "1" ó de "1" a "0" según sea el caso, únicamente durante un instante del ciclo de reloj cuando está ocurriendo la transición entre los niveles lógicos de la señal C. Ciertamente, el tránsito de "0" a "1" o viceversa en la terminal C representa un intervalo de tiempo mucho más corto que la permanencia por un cierto tiempo de dicha terminal en "1" ó en "0". Esto se llama activación en el flanco (edge triggering). El símbolo y un diagrama de tiempos para un flip-flop R-S que trabaje de este modo será el siguiente (obsérvese que en el símbolo que de otro modo sería idéntico al anterior hemos puesto en la terminal C una cuña que representa una transición de nivel, dando a entender que los cambios autorizados solo podrán ocurrir en el instante en que se dé una transición):
En este caso hemos supuesto que los cambios autorizados ocurrirán durante una transición negativa en la terminal C, cuando va de "1" a "0". Podemos modificar este comportamiento haciendo que los cambios autorizados ocurran durante una transición positiva en la terminal C , cuando va de "0" a "1", con el simple remedio de poner un inversor NOT en la terminal C. Obsérvese en el diagrama de tiempos que los cambios en la salida Q del flip-flop ocurren únicamente cuando la señal en la terminal C cae de "1" a "0", una caída tan rápida que no permite que la salida pueda cambiar varias veces cuando se está llevando a cabo la transición.
Además del flip-flop R-S, existen otros elementos de memoria cuyos cambios de estados también son controlados con una entrada de "reloj" C y los cuales también poseen como salidas dos terminales complementarias Q y Q. Y en ellos también es posible encontrar las variantes tanto de activación permisible en cualquier momento al estar en un nivel de "1" o de "0" dependiendo del diseño ó de activación permisible únicamente cuando ocurre una transición de un nivel al otro; la única diferencia en los símbolos convencionales utilizados para distinguirlos es la pequeña cuña puesta dentro de la "caja" cuya ausencia denota que el elemento es activable en cualquier tiempo al estar en cierto nivel:
y cuya presencia indica que el elemento de memoria es activable únicamente cuando ocurre una transición de nivels:
Podemos interactuar con un diseño mejorado del flip-flop R-S que implementa la activación en el flanco con el circuito interactivo ofrecido en la siguiente página:
http://www.play-hookey.com/digital/rs_nand_flip-flop.html
El circuito mostrado en la página citada en realidad es una configuración mejor conocida como la configuración maestro-esclavo (master-slave). Pero esto ya nos lleva a un tema mejor cubierto en el siguiente capítulo en el que se introduce un flip-flop más potente y más versátil que el flip-flop R-S: el flip-flop J-K.





































No hay comentarios:
Publicar un comentario