Para lograr tales elementos con memoria, podemos explotar un fenómeno muy peculiar a los circuitos lógicos de enorme importancia: La retroalimentación (o el regreso) de la salida (o salidas) a la entrada (o entradas) de los circuitos lógicos introduce memoria en los mismos; esto es, se convierten en elementos capaces de almacenar información por tiempo indefinido. (En la literatura de habla inglesa, a la retroalimentación se le conoce como feedback.)
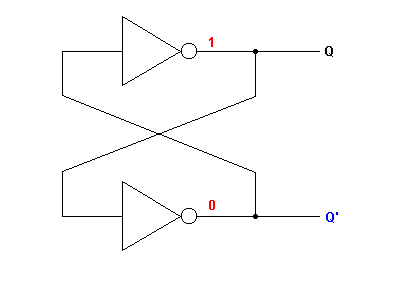
Empezaremos nuestra introducción a los circuitos lógicos capaces de exhibir capacidades de memoria con la siguiente configuración que puede parecer curiosa al principio por carecer por completo de entradas que podamos variar a nuestro antojo:
Para analizar este tipo de circuitos, procedemos exactamente de la misma manera como lo hicimos con los circuitos lógicos combinatorios, en los cuales aplicamos todas las combinaciones posibles de "unos" y "ceros" a la entrada (o entradas) y obtuvimos todas las respuestas posibles a la salida (o salidas) de tales circuitos lógicos, construyendo Tablas de Verdad para cada uno de ellos, análisis que posteriormente fue refinado con la introducción del álgebra Boleana. La diferencia en este caso es que como estamos retroalimentando las salidas a las entradas, no sólo tenemos que aplicar todas las combinaciones posibles de "unos" y "ceros" a la entrada (o entradas) sino que tenemos que aplicar también todas las combinaciones posibles de "unos" y "ceros" a la salida (o salidas), fijándonos muy bien en aquellas combinaciones de entradas y salidas que produzcan estados incompatibles para proceder a desecharlas de nuestro análisis. Un estado incompatible en el anterior circuito formado con dos bloques NOT sería el estado en el cual Q=0 y Q'=0:
Aquí la verificación de que este es un estado incompatible es un asunto fácil. Suponiendo que la salida del NOT superior es "0", entonces dicho "0" está siendo introducido al NOT inferior, el cual por la acción inversora debería convertir dicho "0" produciendo un "1" a su salida, lo cual es incompatible con el "0" que habíamos supuesto desde un principio para Q'. Y si la salida del NOT inferior es "0", entonces dicho "0" está siendo introducido al NOT superior, el cual por la acción inversora también debería convertir dicho "0" en un "1", lo cual es incompatible con el valor que habíamos supuesto de Q=0.
Llevando a cabo un análisis similar, podemos proceder a desechar también el estado Q=1 y Q'=1 como un estado posible, porque también nos produce incompatibilidades. Tal estado simple y sencillamente no puede existir.
Sin embargo, un estado que sí es posible es el estado Q=1 y Q'=0:
Aquí, el "1" que posee la salida Q en el NOT superior es alimentado a la entrada del NOT inferior, el cual por la acción inversora del NOT es convertido a un "0", que es precisamente el valor que estamos suponiendo para Q'. Aquí no hay incompatibilidad alguna. Y el "0" que posee la salida Q' en el NOT inferior es alimentado a la entrada del NOT superior, el cual por la acción inversora del NOT es convertido a un "1", que es precisamente el valor que estamos suponiendo para Q. No habiendo incompatibilidad alguna, aceptamos el hecho de que este es un estado posible y estable.
Pero la combinación Q=1 y Q'=0 no es la única combinación estable para este circuito. Existe otra combinación, la combinación de salidas Q=0 y Q'=1:
la cual también podemos comprobar que también es una configuración estable.
Esto nos conduce a un dilema. Si tenemos dos estados estables, igualmente posibles, tomando en cuenta que el circuito lógico no tiene entrada alguna sobre la cual podamos ejercitar algún control a nuestra discreción, ¿cuál de los dos estados tomará el circuito al encenderse la configuración con la aplicación de energía eléctrica?
La difícil realidad es que, como ambos estados son igualmente posibles, el estado en que podrá caer este circuito al aplicar energía eléctrica es completamente una cuestión de azar. Una vez que se encienda el circuito, podemos encontrarnos con cualquiera de los dos estados, esto es algo que está completamente fuera de nuestro control. Y peor aún, entre estos dos estados existe un tercer estado, conocido como estado meta-estable, en el cual las salidas dejan de ser "0" ó "1" para quedar atoradas en un limbo. Este circuito formado por dos NOTs ciertamente posee memoria, pero su comportamiento azaroso lo vuelve inútil para una aplicación práctica que no sea la de construír una máquina electrónica de juegos de azar. Sin embargo, el circuito nos dá una pista sobre cómo utilizando funciones lógicas más elaboradas que el NOT, tales como bloques NAND o bloques NOR, podemos construír circuitos lógicos con memoria sobre los cuales podamos tener algún tipo de control.
Usando como base tales propiedades, apareció en el mercado por vez primera un elemento básico de memoria conocido como el flip-flop R-S, el cual frecuentemente se representa como una "caja negra" cuyos detalles interiores están ocultos de la vista de los técnicos que atienden sistemas construídos con circuitos lógicos:
Como podemos ver en su representación esquemática, el flip-flop R-S es un bloque fundamental que consta de dos terminales de entrada, la terminal de "ajuste" S (set) y la terminal de "reajuste" R (reset); así como dos terminales de salida Q y Q', las cuales, como su notación lo indica, son complementarias, son el inverso la una de la otra. La palabra combinada "flip-flop" viene del inglés empezando con la palabra flip que es utilizada cuando se usa un interruputor de encendido para prender algo como las luces de la sala de la casa, situación en la que se acostumbra decir "flip the switch", mientras que la palabra flop, derivada de la palabra flip, tiene una intención opuesta, usándose cuando se va a apagar algo a través del mismo interruptor de encendido.
Las características del flip-flop R-S son las siguientes, suponiendo que al empezar ambas entradas R y S estaban siendo alimentadas con un cero (0) lógico:
(1) Cuando S=1 y R=0; o sea, al poner un 1 en la terminal de entrada S, el flip-flop R-S entra en el estado Q=1 independientemente del valor que Q haya tenido anteriormente. La salida Q' a su vez adquirirá el valor Q' =0.
(2) Cuando S=0 y R=1; o sea, al poner un 1 en la terminal de entrada R, el flip-flop R-S entra en el estado Q=0 independientemente del valor que Q haya tenido anteriormente. La salida Q' a su vez adquirirá el valor Q' =0. En lenguaje vulgar, se dice que el flip-flop R-S es reseteado.
Dependiendo de los elementos usados para construír el flip-flop R-S, éste tendrá una combinación de valores S y R con la cual mientras haya suministro de energía retendrá por tiempo indefinido la información que le fué colocada anteriormente.
Desgraciadamente, tendrá también otra combinación de valores que lo colocarán en un estado no-definido en el cual las salidas Q y Q' dejarán de ser complementarias. Esta combinación de valores debe evitarse a toda costa.
Este elemento, como todos los demás bloques fundamentales en los circuitos lógicos, se puede construír empleando funciones lógicas básicas. En general, el flip-flop R-S se construye empleando ya sea funciones NAND o funciones NOR.
Una forma de analizar el comportamiento "interno" del flip-flop R-S cuando es construído a partir de funciones lógicas básicas es considerar para cada combinación de unos y ceros a la entrada todas las combinaciones posibles de unos y ceros a la salida, eliminando sistemáticamente las combinaciones de unos y ceros que no sean compatibles. Este método resulta algo laborioso.
La forma más efectiva de analizar un flip-flop R-S es obteniendo las salidas Q yQ' en función de las entradas R y S utilizando álgebra Boleana. Este método resulta más rápido, más práctico y más académico. De cualquier modo, en la sección de problemas resueltos se usan ambos métodos con el fin de que se pueda comparar las ventajas y desventajas de ambos.
El flip-flop R-S, capaz de almacenar un "bit" de información, se puede utilizar a su vez como bloque básico para construír memorias más complejas tales como la Memoria de Acceso al Azar (Random Access Memory o RAM). La gran mayoría de los lectores debe poder reconocer este tipo de memoria, la famosa memoria RAM; es la que se anuncia en los modelos de las computadoras caseras puestos a la venta con la garantía de que entre mayor sea la memoria RAM mejor podrá ser el desempeño de la computadora.
Aquí se vuelve necesario hacer una aclaración. Aunque es posible almacenar un "bit" o varios "bits" de información usando para ello elementos de memoria construídos con funciones lógicas básicas, se pueden construír elementos de memoria sin utilizar para el almacenamiento de información elemento alguno que involucre alguna de las funciones lógicas básicas, inclusive sin utilizar tecnología de semiconductores. Tal es el caso de las memorias de ferrita magnética (core memory) en las cuales el almacenamiento de un "0" ó de un "1" se lleva a cabo en base a la dirección del campo magnético del elemento utilizado como medio de almacenamiento. El principio esencial radica en que es posible magnetizar una pieza de material magnético en dos direcciones opuestas, como lo muestran los siguientes dos imanes acomodados en direcciones contrarias:
En el imán de la izquierda (A) tenemos su "polo Norte" (N) apuntando hacia la derecha y su "polo Sur" (S) apuntando hacia la izquierda, en una alineación que llamaremos un "0" lógico, mientras que en el imán de la derecha (B) tenemos su "polo Norte" apuntando hacia la izquierda y su "polo Sur" apuntando hacia la derecha, en una alineación que llamaremos un "1" lógico. De hecho, podemos ver esto como el mismo imán acostado en dos diferentes direcciones.
Es un hecho físico bien conocido que con la aplicación externa de una corriente eléctrica es posible magnetizar ciertos materiales en direcciones opuestas, dependiendo de la dirección de la corriente, lo cual a su vez depende de cómo se aplican las polaridades del voltaje que produce la corriente eléctrica:
Este es el mismo principio físico que fue utilizado por Jay W. Forrester en 1952 para inventar las memorias de acceso aleatorio RAM basadas en el uso de ferritas magnéticas, en las cuales utilizó núcleos de ferrita (cores) en forma de anillos y en las cuales la dirección del campo magnético dentro de los anillos podía ser "en sentido del avance de las manecillas del reloj" o "en sentido contrario del avance de las manecillas del reloj" dependiendo de la dirección del flujo de la corriente eléctrica en el alambre puesto en el centro de la ferrita:
En la siguiente fotografía amplificada tenemos un arreglo rectangular de 4 por 4 núcleos de ferrita magnética capaces de almacenar un modesto total de 16 bits (es necesario tomar en cuenta que cada uno de los núcleos de ferrita es de tamaño milimétrico):
Como podemos ver en la fotografía, cada uno de los núcleos de ferrita es atravesado por dos alambres, un alambre horizontal y un alambre vertical que actúan como selectores, lo cual permite localizar un núcleo de ferrita específico entre todos los demás seleccionando eléctricamente el alambre horizontal y el alambre vertical que lo atraviesan. Este método de selección basado en un arreglo rectangular de coordenadas X y Y es completamente general y aplica también a las memorias RAM contemporáneas hechas a base de semiconductores.
En la fotografía no se muestra un tercer alambre que atraviesa a todos los núcleos de ferrita, identificado en aquellos tiempos como el alambre de detección de información Sense y utilizado precisamente para poder "escribir" ó "leer" el "1" ó el "0" almacenado en cada núcleo de ferrita. Porque no basta con poder localizar un núcleo de ferrita individual entre muchos otros, es necesario tener alguna forma de poder meter y sacar la información del mismo:
Inclusive para aquellos tiempos, 16 bits era una cantidad demasiada modesta de "bits" con la cual no se podía hacer prácticamente nada que valiera la pena. Para poder ser de utilidad alguna, era necesario construír arreglos mucho más grandes de núcleos de ferrita magnética, como el siguiente modelo capaz de poder almacenar 2,048 palabras de 8 bits cada una (ampliar imagen):
Dadas las enormes dificultades para poder construír memorias RAM de este tipo, tanto por lo laborioso de la inserción individual de alambres muy delgados (susceptibles de reventarse durante el proceso de inserción) dentro de núcleos de ferrita milimétricos, como por el enorme trabajo involucrado en tener que desarmar toda la configuración para volver a comenzar de nuevo en caso de que un solo núcleo de ferrita resultara defectuoso, el costo de una memoria como esta ascendía fácilmente a los cientos de miles de dólares aunque la fabricación se llevara a cabo en países asiáticos con mano de obra sumamente barata. Esta es una de las razones por la que en esos tiempos las computadoras no se vendían, se rentaban, e inclusive así los costos de la posesión temporal de las mismas podían ser sumamente elevados. Pese a todo, esta era la memoria RAM utilizada en el 95 por ciento de todas las computadoras empresariales (las computadoras personales de escritorio no existían aún) usadas hasta 1976. La situación eventualmente cambiaría al hacer su aparición en 1970 la primera memoria RAM construída con semiconductores, la memoria dinámica RAM 1103, con una capacidad de almacenamiento de 1,024 bits, construída por una nueva empresa que nació viendo una posibilidad de que los semiconductores eventualmente pudieran reemplazar algún día los costosos núcleos de ferrita magnética, Intel:
No hay comentarios:
Publicar un comentario