en lugar de construírlo a partir de las tres funciones lógicas básicas se desea utilizar un circuito integrado Selector de Datos obtenible a bajo costo en el mercado, en el cual las líneas selectoras S0, S1 y S2 se utilizarán como las entradas A, B y C, y las líneas de datos se activarán de modo fijo con "unos" y "ceros". Resolver este problema usando:
1) Un Selector de Datos 1-de-8
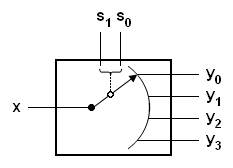
2) Un Selector de Datos 1-de-4
1) Usando un selector de datos 1-de-8, la solución es directa:
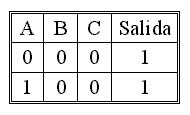
Según se puede ver, al tomar la entrada ABC la condición "000", el primer valor en la lista "1" pasa a la salida. Al tomar ABC la condición "001", el segundo valor "1" en la lista pasa a la salida. Y así sucesivamente. Obsérvese que los valores sucesivos que deberá tener la salida siguiendo un conteo binario ascendente en las entradas selectoras fueron tomados directamente de la Tabla de Verdad.
2) Para llevar a cabo una simplificación con la cual podamos utilizar un Selector de Datos más sencillo que tenga únicamente dos entradas selectoras, agrupamos primero pares iguales sucesivos de B y C y comparamos la salida de cada par con los valores que debe tomar A a la entrada según la Tabla de Verdad:
Aquí la salida siempre será "1" independientemente del valor que tome la entrada A.
En este caso podemos ver que la salida es el complemento (el inverso lógico) de la entrada A.
En este caso, la salida siempre será "0" no importando el valor que tome A.
Aquí la salida tomará el mismo valor que tome la entrada A.
Tomando en cuenta lo anterior, usando un Selector de Datos 1-de-4 el diseño tomará el siguiente aspecto:
o más concretamente, en el diseño final:
Obsérvese lo sencillo y económico que resulta diseñar circuitos lógicos usando un Selector de Datos. El procedimiento empleado en el presente problema se puede extender a más variables sin dificultad alguna. Aunque un Selector de Datos 1-de-16 como el circuito integrado TTL 74150 es más caro que un Selector de Datos 1-de-4 como el circuito integrado TTL 74151, la diferencia en costo quizá no sea tanta para justificar irse al diseño más económico como lo hicimos en este caso simplificando el diseño de modo de requerir un Selector de Datos 1-de-4 en lugar de un Selector de Datos 1-de-8, tomando en cuenta que la lógica detrás del diseño simplificado será más difícil de leer para los técnicos que le darán mantenimiento a un equipo utilzando el diseño simplificado. Por otro lado, si se van a producir decenas de miles de equipos que serán puestos a la venta en el mercado, entonces una diferencia de precio de unos cuantos centavos entre un circuito integrado y otro puede traducirse en un ahorro significativo de varios miles de dólares.
PROBLEMA: La siguiente unidad, conocida comúnmente como como unidad demultiplex (DMUX) envía la información puesta a su entrada únicamente a uno de los cuatro canales de salida.
El canal deseado es seleccionado usando la palabra binaria A1A0 como selector. ¿Cuál es su configuración interna? Extender el diseño para una unidad demultiplex que pueda ser capaz de enviar su entrada a uno de ocho canales de salida.
La configuración interna es como la que se muestra a continuación:
La acción de "switcheo" requerida del bloque DMUX es esencialmente la siguiente:
Una forma de representar la configuración interna de la unidad DMUX en donde sigue existiendo la presencia interna de un "decodificador" de S1S0 aunque de una manera no tan obvia es la siguiente:
En esta representación, se sigue llevando a cabo una decodificación de la palabra binaria S1S0 convirtiéndola en una de cuatro líneas independientes para cada una de las cuatro combinaciones de "unos" y "ceros" puesta en S1S0, con el propósito de permitir el paso por solo uno de los cuatro bloques AND en un momento dado. Sin embargo, puesto dentro de una "caja negra", este circuito es enteramente equivalente al anteriormente mostrado. Este último diseño puede ser extendido para manejar ocho canales de salida con la adición de una terminal selectora adicional S2 con la cual la palabra selectora será S2S1S0, y la adición de cuatro bloques AND adicionales también de tres entradas cada uno (ampliar imagen):
Una forma de representar simbólicamente a una bloque demultiplex DMUX en los diagramas esquemáticos que conlleva la idea de lo que está realizando (una función opuesta a la función realizada por el bloque MUX) es de la siguiente manera:
PROBLEMA: Describir el funcionamiento conjunto de una unidad multiplex con una unidad demultiplex.
En la vida real, invariablemente cuando en un sistema se usa una unidad multiplexora MUX es porque irá apareada siempre con una unidad demultiplexora DMUX, y ambas deberán trabajar de modo conjunto a través del selector que actuará al mismo tiempo y en forma sincronizada sobre ambas unidades MUX y DMUX de la siguiente manera:
La razón obvia para tener que recurrir a una operación combinada MUX-DMUX es porque frecuentemente es necesario enviar (o recibir) información proveniente de diversos equipos cuando sólo hay un canal de comunicación disponible para la transmisión digital. Un ejemplo de esto lo serían varias computadoras conectadas desde un mismo lugar a Internet, compartiendo una sola línea telefónica. Como la información digital de varias computadoras no puede ser enviada al mismo tiempo por un solo canal de comunicación, el tiempo disponible del canal es "repartido" en partes iguales, dándole un tiempo breve a la computadora # 1, tras lo cual se le dá un tiempo breve a la computadora # 2, y así sucesivamente, tras lo cual vuelve a comenzar una nueva ronda dándosele un tiempo breve a la computadora # 1 seguida por la computadora # 2, y así sucesivamente.
Desde el punto de vista de la unidad multiplexora MUX, la información irá saliendo de una manera como se muestra a continuación:
Esquemáticamente, en este circuito lo primero en salir, lo primero en ser puesto en la única línea disponible para la transmisión externa de los datos, es el primer dato "A" representado por un triángulo rojo en el extremo superior izquierdo, el primer dato en el primer canal de comunicación. Tras esto, se envía a través de la línea el segundo dato "B" representado por el primer paralelogramo verde tomado del segundo canal de comunicación , el primer dato en el segundo canal de comunicación. A esto le sigue el dato "C" tomado del tercer canal de comunicación identificado con un círculo azul. Por último, se envía un dato "D" tomado del cuarto canal de comunicación, representado con un rombo color magenta, tras lo cual el ciclo empieza de nuevo. Obsérvese cómo marchan "aparentemente" revueltos los datos a través de la única línea disponible para la transmisión externa de datos. Para obtener algún sentido de los datos que están siendo enviados, el receptor tiene que estar forzosamente sincronizado con el envío de los datos. Es por ello que los selectores del MUX y del DMUX tienen que estar conectados de alguna manera, para ir ruteando (routing) la información por los canales adecuados sin que haya posibilidad de que termine revuelta.
La acción sincronizada selectora MUX-DMUX se muestra bosquejada en el siguiente archivo GIF (ampliar imagen para poder ver la acción animada):
PROBLEMA: La Tabla de Verdad de un circuito electrónico muestra los siguientes valores de voltaje, tanto para las entradas A y B como para la salida producida. ¿Qué función desempeña el circuito en lógica positiva? ¿Qué función desempeña en lógica negativa?
Usando lógica positiva, asignamos al voltaje más pequeño (o más cerca de cero volts, o el más negativo) el valor de "0" y al voltaje mayor (en este caso 3.2 volts) el valor de "1":
Esta es una función NOR.
Usando lógica negativa, asignamos al voltaje mayor el valor de "0" y al voltaje más pequeño el valor de "1", o sea lo contrario que lo que hicimos anteriormente:
Esta es una función NAND.
PROBLEMA: El circuito mostrado a continuación recibe el nombre de "compuerta" en un sentido diferente al que frecuentemente se les dá a los bloques lógicos AND, OR y NOT. ¿Qué acción se lleva a cabo de acuerdo con el valor que tome la terminal T?
Dada la acción de las funciones AND, cuando la terminal T toma el valor "0", la salida de la compuerta es "000000". Cuando la terminal T toma el valor "1", la salida de la compuerta es A6A7A5A4A3A2A1. Esto es, la terminal T está actuando como un gatillo que detiene o permite el paso de la información según el valor que adquiera. Supóngase que
A6A7A5A4A3A2A1 = 100110
Entonces tendríamos los siguientes casos:
PROBLEMA: Analizar el siguiente circuito construyendo una Tabla de Verdad para el mismo.
En el análisis de este tipo de circuitos, resulta conveniente buscar aquellas combinaciones de entradas que siempre produzcan un resultado consistente independientemente de los valores que tomen las demás entradas. Para ir "llenando" nuestra Tabla de Verdad inicialmente en blanco, podemos llenar toda la columna que corresponde a los valores de la salida I dándonos cuenta de que esta salida está conectada directamente a la entrada D, de modo tal que cuando la entrada D sea "0" la salida E será también "0" y cuando la entrada D sea "1" la salida E será también "1". Del mismo modo, podemos ver que la acción del AND de tres entradas que proporciona la salida F solo producirá un "1" a la salida de F cuando tenemos ABC=100 tanto para D=0 como para D=1, lo cual nos permite llenar toda la columna correspondiente a la salida F de inmediato con "unos" y el resto con "ceros". Asimismo, cuando la entrada A tiene el valor de "1", abriendo con ello la compuerta que representa el AND que proporciona la salida E, basta con que cualquiera de las entradas B ó C tengan el valor de "1" para que la salida E tenga también un "1", y solo cuando ambas entradas tengan un valor de "0" la salida será "0". Puesto de otra manera, todas las combinaciones para las cuales A=1 y B=1 "encienden" la salida E, y todas las combinaciones para las cuales A=1 y C=1 también "encienden" la salida E. Cuando ambas entradas B y C sean "0" la salida E siempre será "0". En lo que respecta a la salida G, esta requiere que la entrada B sea "1" y que además A sea "0" o que C sea "1" para que la salida G se "encienda" con un "1". Y en lo que respecta a la salida H, esta será "1" únicamente cuando las entradas A y C tengan el valor AC=01 (por la acción del primer AND que alimenta al OR de la salida I) o cuando las entradas A, B y C tengan el valor ABC=110 (por la acción del segundo AND que alimenta al OR de la salida I), siendo "0" en todos los demás casos. Así podemos ir llenando una Tabla de Verdad sin necesidad de tener que ir considerando individualmente cada combinación posible de "unos" y "ceros" a la entrada, con lo cual eventualmente podemos tener la siguiente Tabla de Verdad terminada:
Comparando la entrada ABCD al circuito (tomando las entradas juntas como una palabra binaria) con la salida EFGHI, observamos una cosa muy interesante: la salida del circuito es idéntica a la entrada desde ABCD=0000 hasta ABCD=1001 (lo cual es un conteo binario ascendente), tras lo cual desde ABCD=1010 en adelante la salida empieza a "contar" nuevamente en forma binaria ascendente partiendo otra vez desde "cero". Puesto de otra manera, la salida nos está dando el número binario puesto a la entrada convertido a su equivalente en sistema BCD. Si conectáramos la palabra FGHI a una carátula decimal numérica (usando un decodificador como el descrito en un problema anterior), estaríamos leyendo en nuestro sistema decimal el equivalente del número binario puesto a la entrada. La salida E cuando se "enciende" con un "1" es la que se utiliza para indicar que estamos en un nuevo conteo decimal, y se podría utilizar también para "encender" un segundo indicador luminoso correspondiente a las decenas de nuestro sistema decimal.Este circuito es un ejemplo de lo que se conoce como un traductor, en este caso un traductor de binario a BCD.
PROBLEMA: A continuación se presenta el diagrama esquemático de una punta de prueba lógica de construcción económica que puede ser utilizada para confirmar la presencia de un "0" o de un "1" en un punto cualquiera de un circuito lógico. Explicar el funcionamiento de la misma.
Aunque el diagrama indica que la punta de prueba lógica debe ser alimentada con una fuente de voltaje de +12 volts, en realidad no se requiere una fuente de poder externa independiente, ya que la práctica usual es alimentar estas puntas de prueba tomando energía eléctrica del mismo circuito que está siendo analizado.
La información de entrada a la punta de prueba se encuentra en la punta denominada probe, en la cual se puede poner un "0" o un "1" según la condición lógica del punto que está siendo medido. Esta información será puesta a la entrada de un NOR en la terminal # 1 del circuito integrado (IC1a) 4001 que está siendo utilizado para la entrada. Puesto que la otra terminal # 2 del circuito integrado está colocada en el nivel de cero volts, lo cual es un "0" lógico, lo único que cambiará la salida del NOR será el valor puesto en su terminal # 1. Si en la punta "probe" hay un "0" entonces la salida del NOR en su terminal # 3 será "1", y si en la punta "probe" hay un "1" la salida del NOR será "0".
La terminal de salida # 3 del bloque NOR alimenta una de las terminales de entrada del otro bloque NOR (IC1b), en el cual puesto que su otra entrada está conectada a 0 volts está siendo utilizado simplemente como un inversor lógico de la señal enviada por el NOR que le precede.
Siguiendo la ruta de valores binarios, si el valor en "probe" es "0", la salida del NOR a la derecha será también un "0", lo cual equivale a poner el punto intermedio entre las resistencias eléctricas a cero volts. Esto hace que la corriente eléctrica fluya de la fuente de poder a través del diodo emisor de luz verde LED1 (LO) continuando hacia la terminal de entrada # 4 del bloque NOR (el "0" a la salida del NOR posibilita que la corriente eléctrica pueda fluír hacia adentro del NOR, ya que la corriente eléctrica siempre fluye del polo positivo ó "1" al polo negativo ó "0") en vez de fluír a través del diodo emisor de luz LED2 rojo que permanecerá apagado. La corriente eléctrica estará limitada por la presencia de la resistencia superior de 680 ohms cuyo valor es justo lo que se requiere para que el LED del diseño pueda iluminarse adecuadamente. En esencia, con un "0" a la entrada de "probe", se encenderá el LED verde indicando una condición lógica de "0" ó LO (bajo).
La situación cambia cuando en "probe" está puesto un "1", lo cual hace que también en la terminal # 4 del NOR derecho haya un "1" que podemos tomar como esencialmente igual al voltaje de +12 volts. Puesto que ambos extremos del diodo emisor de luz verde LED1 están ahora al mismo potencial eléctrico de +12 volts, no puede fluír corriente alguna a través del LED verde, el cual estará apagado. En cambio, este "1" estará poniendo un voltaje de +12 volts al diodo emisor de luz rojo LED2, el cual al estar conectado del otro lado al potencial de cero volts tendrá una diferencia de voltaje de 12 volts aplicada entre sus dos terminales, lo cual hará que el LED2 conduzca con la corriente eléctrica limitada por la resistencia de 680 ohms justo a lo que se requiere para que el LED pueda iluminarse adecuadamente. En esencia, con un "1" a la entrada de "probe", se encenderá el LED rojo indicando una condición lógica de "1" ó HI (alto) en el punto que está siendo medido.























2 comentarios:
oye como quedaría el diagrama en circuito impreso, lo podrías poner por favor.
oye como quedaría el diagrama en circuito impreso, lo podrías poner por favor.
el de la punta logica
Publicar un comentario